算法-策略(递归,二叉搜索)
分而治之
一个大问题不断拆成各种小问题,大问题与小问题的方向要一致。
递归函数(递减)
分析时间函数的两种方法:递归树(跟踪树) ,代换法。
例1
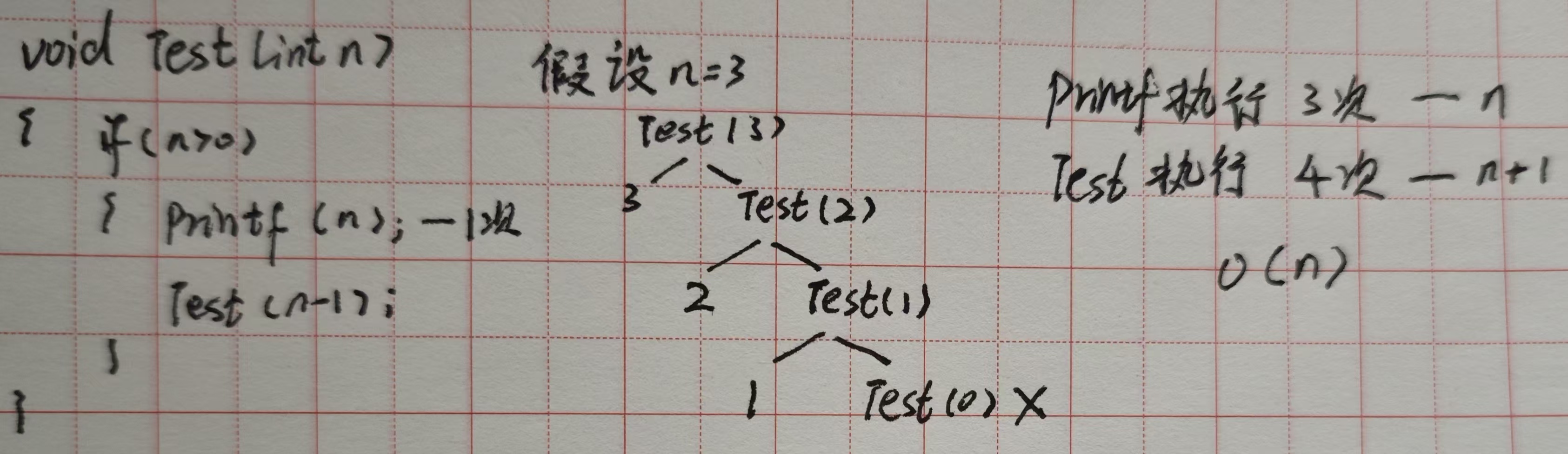

例2
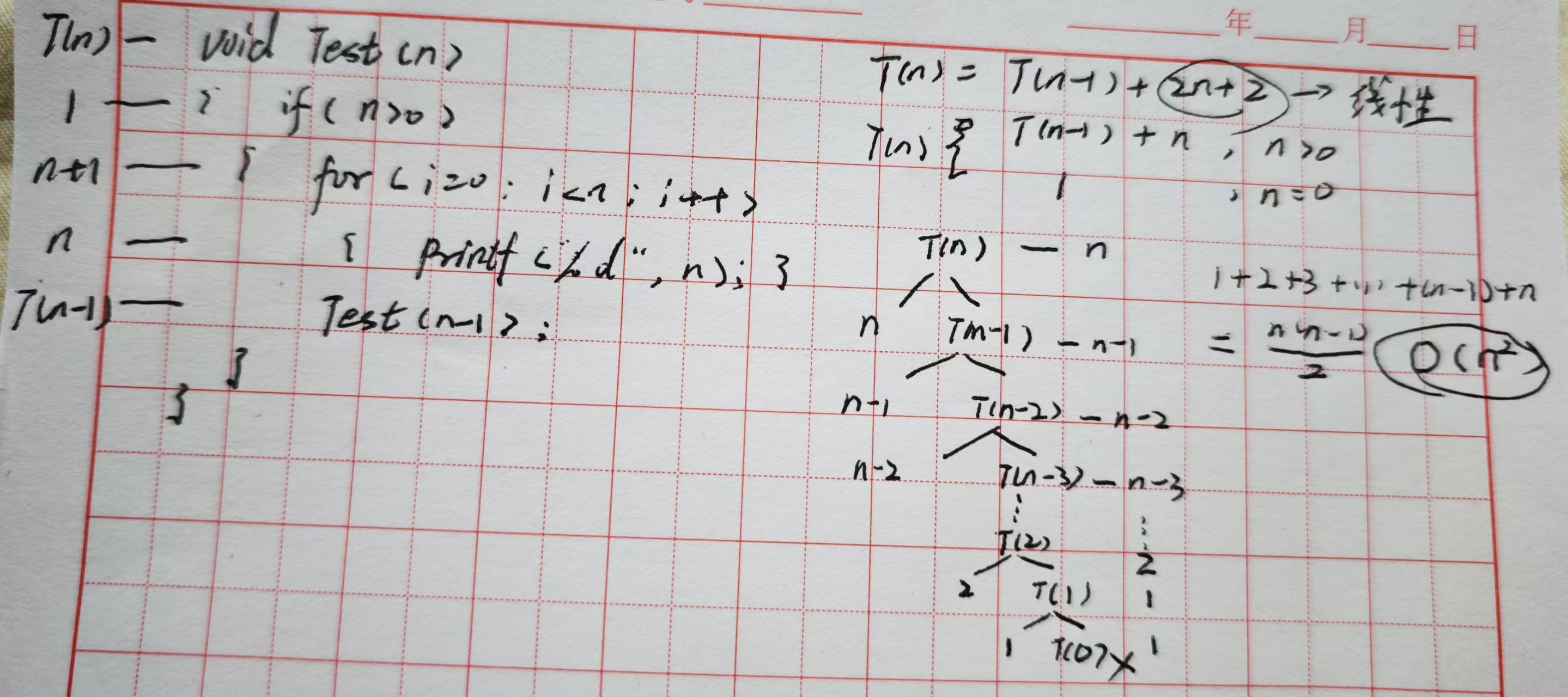
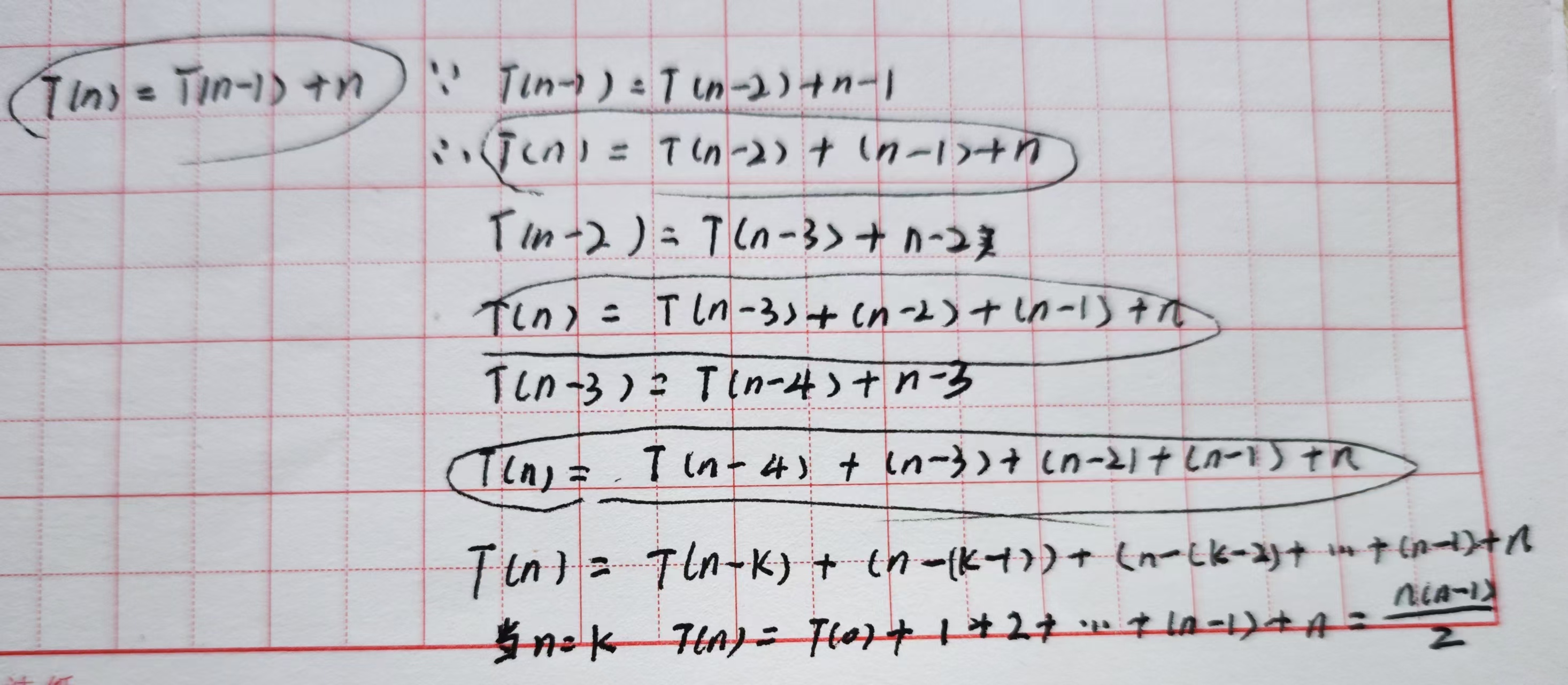
这里的代换法注意,不要轻易的把常数加在一起,加在一起后看不出规律!!!!!!
例3


规律1

例4

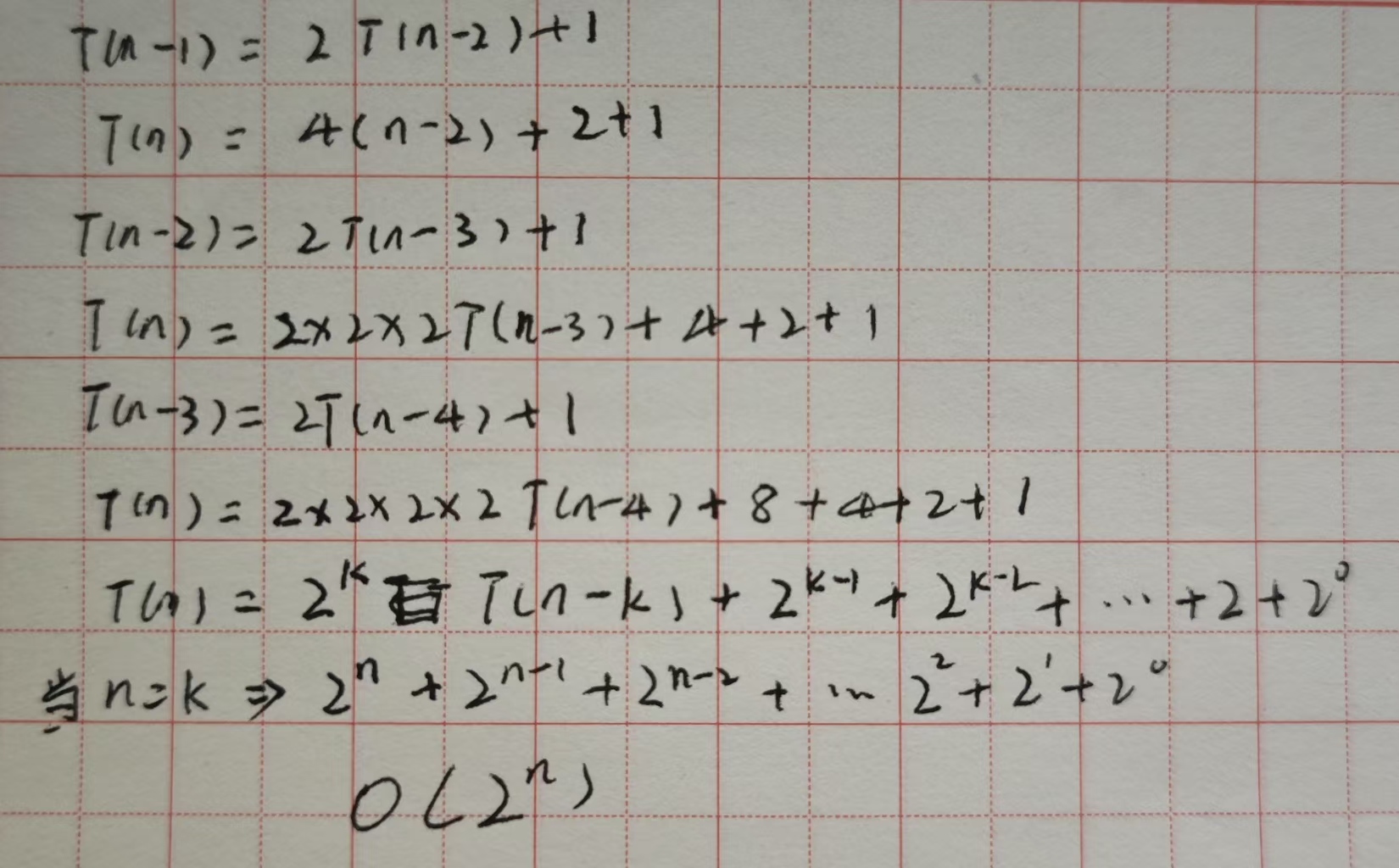
规律2(最终定理!)
递归函数(除法)
例1
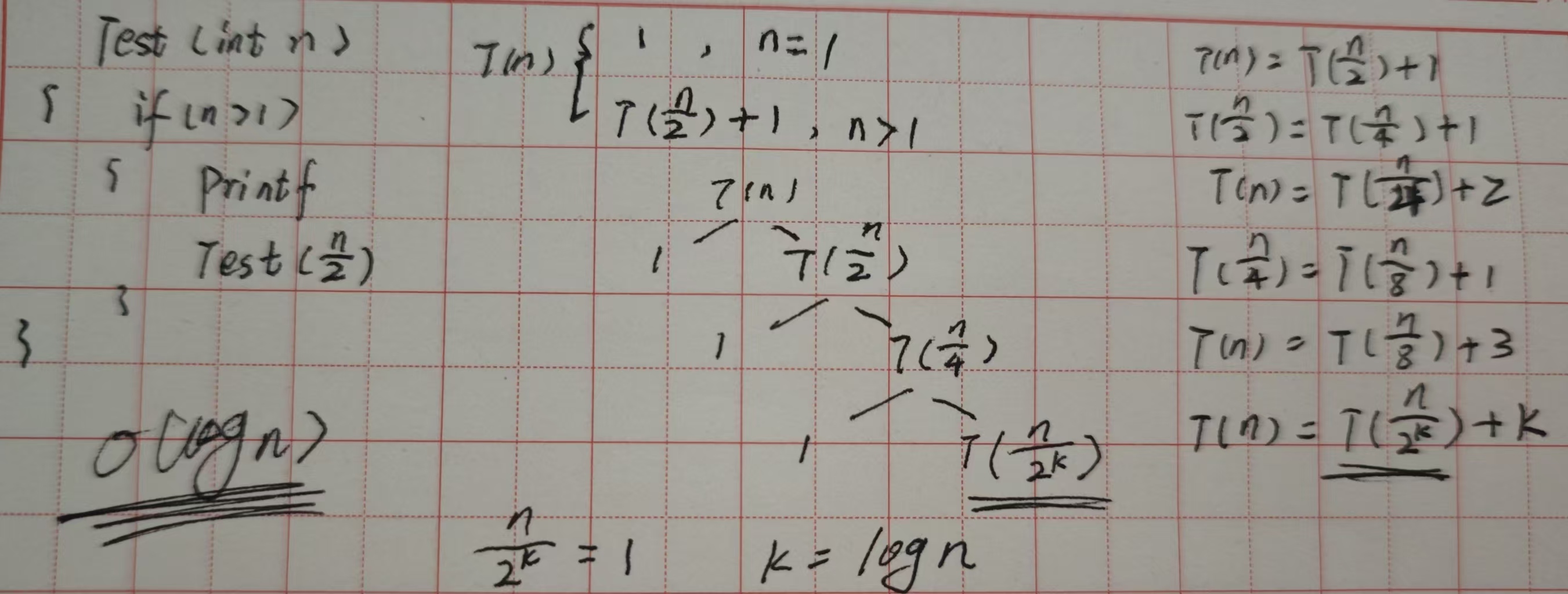
例2
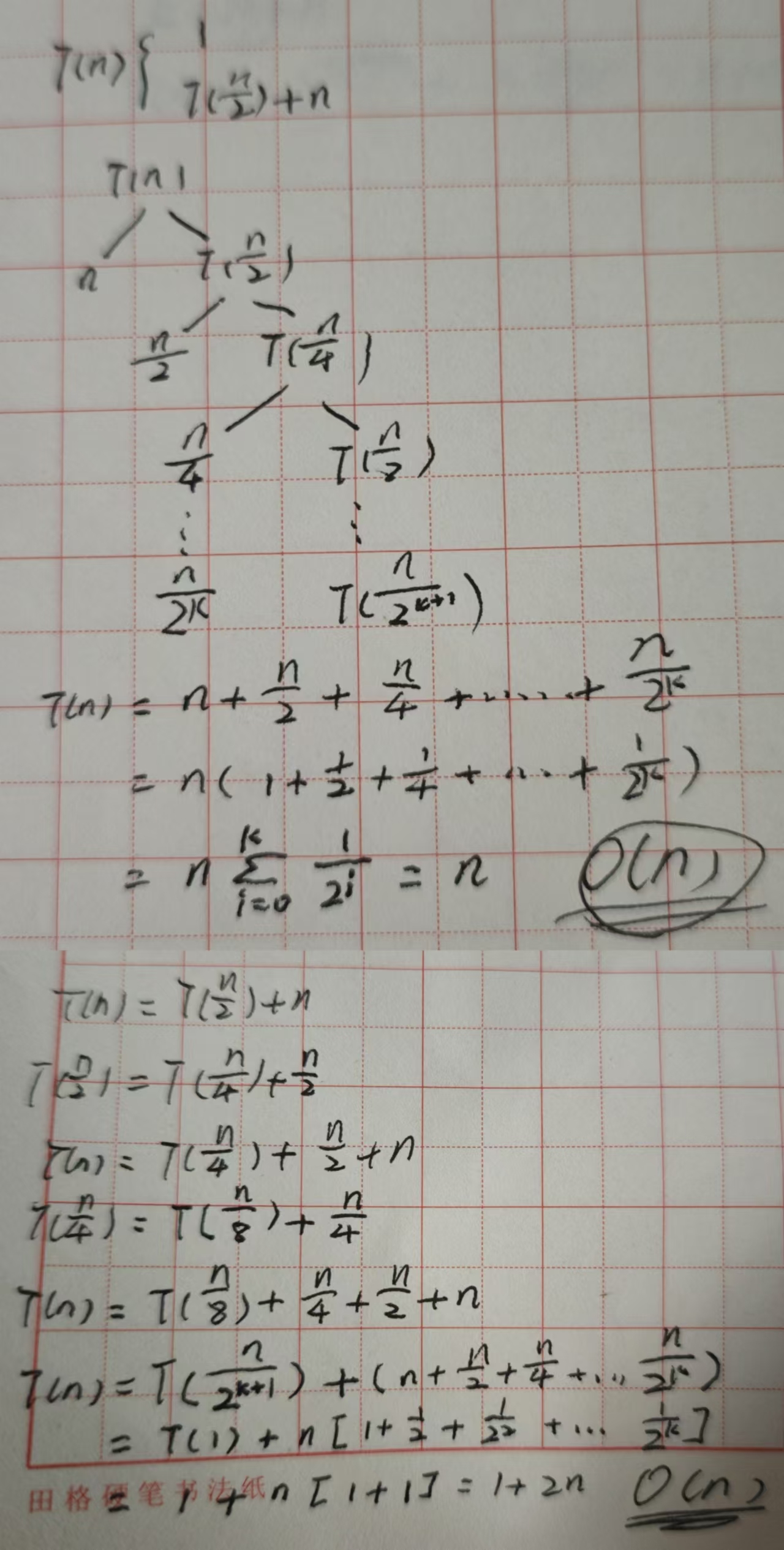
例3

规律!!!

根据规律做几个例子:

递归函数(根函数)
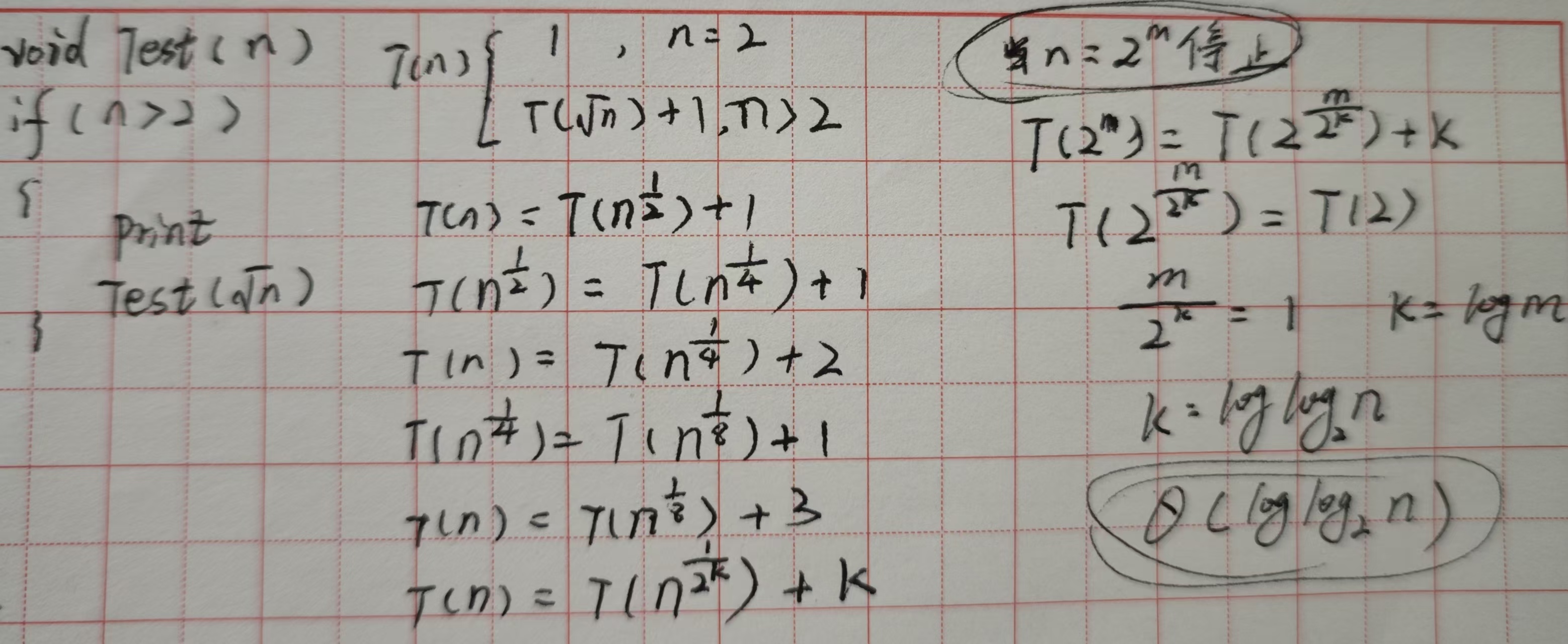
二分搜索迭代法
循环算法
首先要排序!!!例子如下:

算法如下(只是逻辑,不规范):
//A数组,n元素大小,key要搜索的键;返回找到元素的索引
int BinSearch(A,n,key){l=1;h=n;while(l<=h){mid=(l+h)/2if(key=A[mid]){return mid;}if(key<A[mid]){h=mid-1;}else{l=mid+1;}}return 0;
}
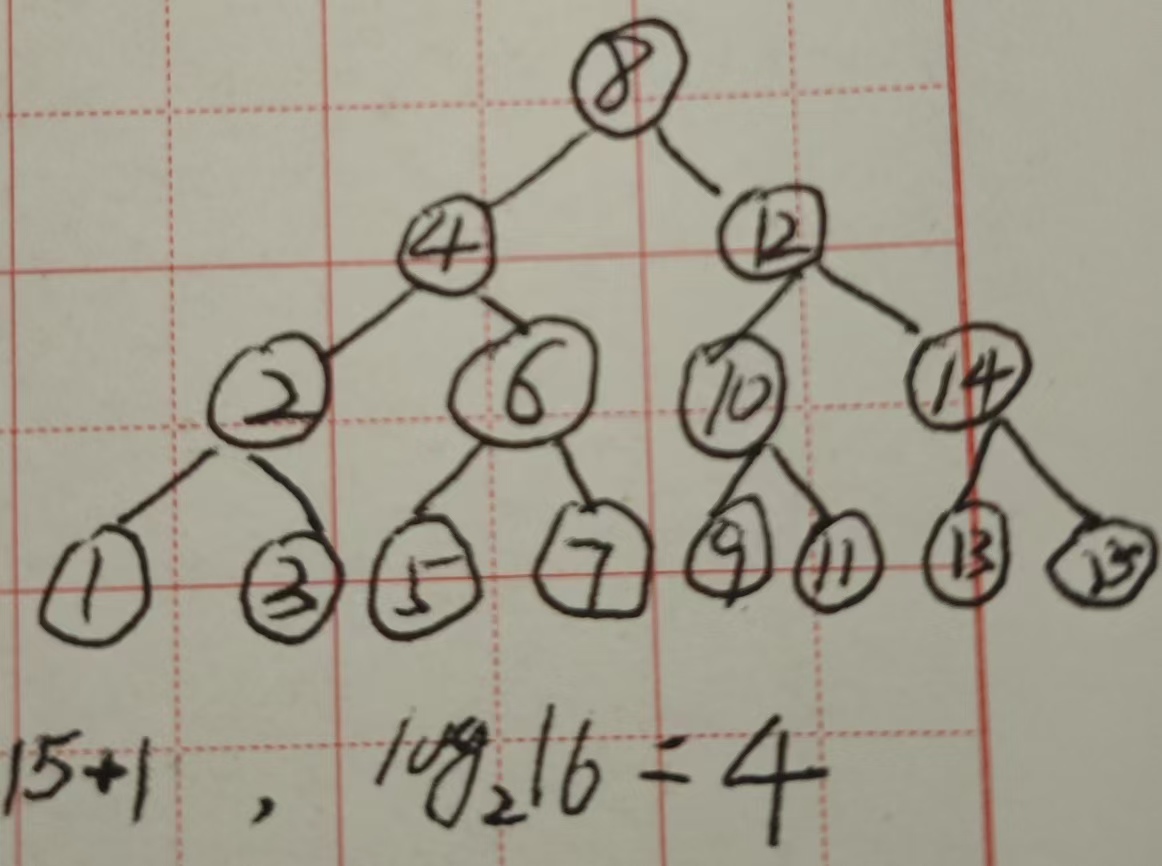
通过树形逻辑来分析 :
二叉搜索的时间复杂度为树深,即logn
图中n为15,加1是因为存在要找的键值不存在于数组中,那么就会有1的存在。
递归算法
Algorithm RBinSearch(l,h,key){if(l==h){if(A[l]==key){return l;}else{return 0;} }else{mid=(l+h)/2;if(key==A[mid]) return mid;if(key<A[mid]) return RBinSearch(l,mid-1,key);if(key>A[mid]) return RBinSearch(mid+1,h,key);}
}
T(n) 1 n=1
T(n/2)+1 n>1
根据前面的定理,时间复杂度为O(logn)
