【数字图像处理】图像纹理分析
图像纹理分析

图像纹理分析概述
纹理定义:图像纹理由图像强度局部变化重复的模式组成,这种重复模式的基本单元(或基元)按某种规则排列
纹理的两个基本要素:
(1)纹理基元
(2)空间关系
纹理的基本特征:区域属性,与图像分辨率(尺寸)相关
纹理分析:通过一定的图像处理技术提取出纹理特征参数,从而获得纹理的定量或定性描述的处理过程
纹理分析的主要内容:
(1)根据视觉感知,用数学模型表示纹理的粗糙性、方向性、重复性、规则性及尺度性等
(2)对纹理特征进行有效提取的方法
(3)纹理分析应用研究,如纹理分类、纹理合成、纹理检索等
纹理分析的方法:
(1)统计法
(2)结构法
(3)模型法
(4)信号处理法

统计法
【1】灰度分布统计
灰度直方图,不能反映空间分布关系,也不能表示纹理的粗糙性和规则性。

【2】灰度共生矩阵
两个位置的像素的联合概率密度。反映亮度的分布特性,反映具有同样亮度或接近亮度的像素之间的位置分布特性
灰度共生矩阵定义:

频度矩阵 归一化后 得到 灰度共生矩阵

【解释一下第一个图的计算过程】
δ(1, 0)中,第0行第0列为6,因为该方向上 0 -> 0 的个数为6,如下图
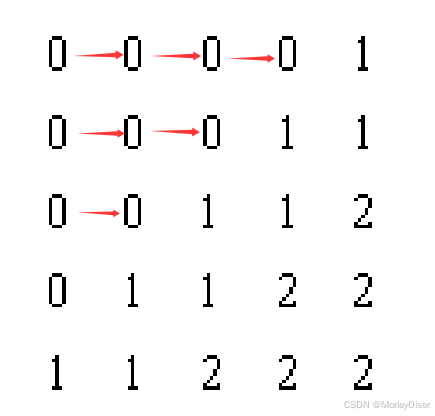
δ(1, 0)中,第1行第1列为4,因为该方向上 1 -> 1 的个数为4,如下图

常用统计量:

(1)角二阶矩或能量:反映图像灰度分布均匀程度和纹理粗细度
(2)对比度:反映图像的清晰度和纹理的沟纹深浅
(3)相关性:反映图像中局部灰度相关性
(4)熵:反映图像纹理的随机性
(5)逆差距:反映矩阵中大值元素到主对角线的集中程度
【3】自相关函数
纹理基元下降速度与纹理的粗糙性(粗细度)有关;纹理细致,则下降迅速
自相关函数:考察某窗口内某一像素和与其偏离一定距离的像素之间的相似程度
自相关函数的周期性反映纹理基元重复出现的现象
结构法
常用方法:
(1)统计量
(2)组合规则分析
树文法:具有一组生成规则(产生式)的树语言(树的集合)产生系统

纹理的树状安排方法:
(1)树根安排在中间,树枝向两边伸出,每个树枝有一定的长度

(2)树根安排在一侧,分枝都向另一侧伸展

对每一个纹理文法可建立一个《结构保存的误差修正树状自动机》
模型法
基于模型法进行纹理分析的关键是准确估计模型的特征参数集
【1】Markov 随机场
随机场:当按照某种分布给每个位置随机赋予相空间的一个值之后的全体
S的领域:

位置i的领域:

势团:邻域系统中的任意两个元素相邻

Markov随机场

Gibbs随机场

二阶邻域的Markov随机场

【2】分形维
分形(Fractal)的主要特征:自相似性、无限细致性、分数维
分形模型:
(1)cantor(康托)三分集
(2)Koch曲线
(3)Julia集
分形维可描述物体表面粗糙度
分形维越大,纹理越粗糙
常用分形维方法:
(1)Hausdorff维
(2)盒子维
(3)修正盒维数
(4)填充维数
盒子维:使用相邻的大小固定的盒子去度量,使用最小数量的欧氏结构体在固定的尺度下来覆盖整个集合

【3】局部二值模式(LBP)

计算:

修正统计变换(MCT):


信号处理法
常用的信号处理法:
(1)傅里叶变换
(2)小波变换
傅里叶变换:
描述近似周期性的纹理图像的方向性
纹理分割
纹理分割:按照一定的纹理特征和一致性属性准则,区分输入图像中不同纹理的过程
常用的纹理分割方法:
【1】基于区域分割方法:阈值法、区域生长和分裂合并法等。
【2】基于边界分割方法:基于微分的边缘检测、基于模板匹配的边缘检测等
