从单模态到多模态：深度生成模型的演进历程

在人工智能领域，生成模型的发展一直是研究热点。从最早的自编码器到如今的多模态扩散模型，这一技术路线不断突破，为创意内容生成、数据增强和表示学习等领域带来革命性变化。本文将详细介绍几种关键生成模型的技术原理和演进路径，展示从单模态到多模态的技术发展历程。

生成模型简介

1. GAN（生成对抗网络，2014年6月)

背景

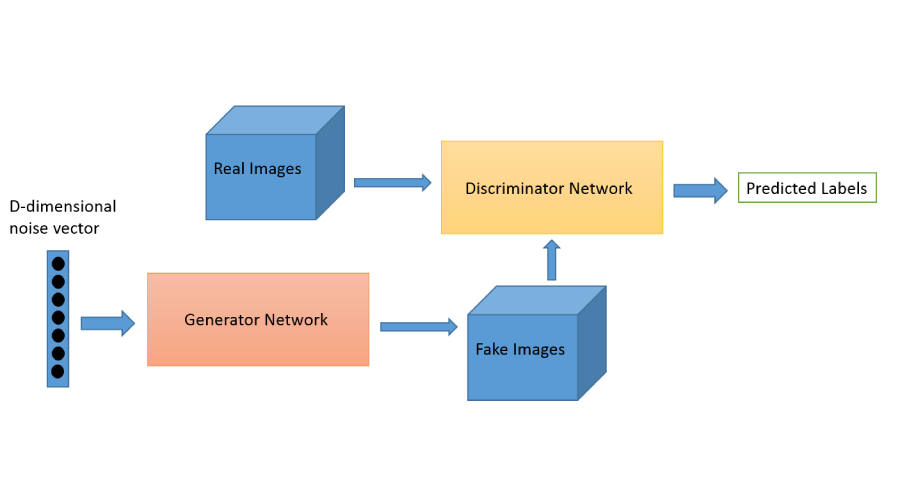
由Ian Goodfellow等人提出，旨在通过对抗训练生成逼真数据。其核心思想是通过生成器与判别器的博弈，使生成器逐渐逼近真实数据分布。

原理

• 生成器（Generator）：将随机噪声$z$映射到数据空间，生成样本$G(z)$。
• 判别器（Discriminator）：判断输入样本是否来自真实数据分布，输出概率$D(x)$。
• 对抗目标：生成器最大化判别器的判断错误，判别器最小化分类误差：
  $$\underset{G}{\min }\underset{D}{\max }{\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$

网络结构

• 生成器：多层全连接或卷积网络，输出与真实数据相同维度的样本。
• 判别器：类似分类器，通常为全连接或卷积网络，输出二分类概率。

优缺点

• 优点：
  • 生成样本质量高，支持多样化生成（如高分辨率图像）。
  • 支持条件生成（如CGAN）。
• 缺点：
  • 训练不稳定（模式崩溃、梯度消失）。
  • 难以评估收敛性，需平衡生成器与判别器的训练速度。

应用场景

• 图像生成（如DeepFakes）、风格迁移（如CycleGAN）、超分辨率重建。

---

2. AE（自编码器，1986年）

背景

经典无监督学习模型，由编码器和解码器组成，目标是学习数据的紧凑表示并重构原始数据。

原理

• 编码器：将输入$x$压缩为低维潜在向量$z=E(x)$。
• 解码器：从$z$重构$x^{\prime }$，最小化重构误差：
  $$\mathcal{L}=||x-D(E(x))|{|}^2$$

网络结构

• 编码器：全连接或卷积层，逐步降低维度。
• 解码器：反卷积或全连接层，恢复原始数据维度。

优缺点

• 优点：
  • 简单高效，适合降维和去噪。
  • 可用于特征提取（如图像压缩）。
• 缺点：
  • 潜在空间无明确结构，生成样本模糊。
  • 不支持直接采样生成新样本。

应用场景

• 数据压缩（如图像压缩）、特征提取、去噪（如图像修复）。

---

3. VAE（变分自编码器，2013年12月）

背景

基于贝叶斯概率框架，通过变分推断学习潜在变量分布，解决AE的潜在空间不连续问题。

原理

• 编码器：输出潜在变量分布参数$\mu ,\sigma$，即$q_{\varphi }(z|x)$。
• 解码器：从$z\sim \mathcal{N}(\mu ,{\sigma }^2)$生成样本。
• 损失函数：重构损失（Reconstruction Loss） + KL散度（正则化）：
  $$\mathcal{L}={\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]-\text{KL}(q_{\varphi }(z|x)||p(z))$$

网络结构

• 编码器：输出均值和方差的两个向量。
• 重参数化技巧：$z=\mu +ϵ\cdot \sigma$, $ϵ\sim \mathcal{N}(0,I)$。

优缺点

• 优点：
  • 潜在空间连续且结构化，支持插值和采样。
  • 可解释性强，适合生成多样化样本。
• 缺点：
  • 生成样本模糊（KL散度惩罚过强）。
  • 重构质量可能下降（如图像边缘模糊）。

应用场景

• 图像生成、语义嵌入、数据增强（如生成相似但不同的样本）。

---

4. VQ-VAE（矢量量化变分自编码器，2017年12月）

背景

为解决VAE生成模糊问题，引入离散潜在空间，结合自编码器与矢量量化技术。

原理

• 编码器：输出连续潜在向量。
• 矢量量化层：将连续向量映射到最近邻离散码本向量$e_k$。
• 解码器：从离散向量重构数据。
• 损失函数：重构损失 + 矢量量化误差（编码器与码本的差异）。

网络结构

• 码本：预先定义的离散向量集合。
• 离散化步骤：$z_q=\arg {\min }_{e_k}||z_e-e_k|{|}^2$。

优缺点

• 优点：
  • 生成样本清晰，避免后验坍塌。
  • 离散空间支持高效检索（如文本生成）。
• 缺点：
  • 离散化可能降低潜在空间的连续性。
  • 训练复杂度增加（需优化码本）。

应用场景

• 图像生成（如DALL·E）、音频合成（如语音编码）、文本生成（如离散化语言模型）。

---

5. Diffusion Model（扩散模型，2015年3月）

背景

受物理扩散过程启发，通过逐步添加噪声再逆向去噪生成数据。

原理

• 正向扩散过程：
  $$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{ϵ}_{t-1},{ϵ}_{t-1}\sim \mathcal{N}(0,I)$$
  其中，${\beta }_t$为噪声调度参数，逐步将数据$x_0$变为噪声$x_T$。
• 逆向生成过程：
  学习模型$p_{\theta }(x_{t-1}|x_t)$从噪声恢复数据。

数学基础

• 正向过程：马尔可夫链，每一步添加高斯噪声。
• 逆向过程：通过深度网络预测噪声${ϵ}_t$，逐步去噪：
  $$x_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\sqrt{1-{\alpha }_t}{ϵ}_{\theta }(x_t,t)\right)$$
  其中，${\alpha }_t=1-{\beta }_t$。

网络结构

• 去噪网络：通常为U-Net，预测当前步的噪声${ϵ}_t$。
• 时间嵌入：扩散步数$t$作为输入，指导去噪。

优缺点

• 优点：
  • 生成质量高，支持条件生成（如文本到图像）。
  • 理论基础扎实，避免模式崩溃。
• 缺点：
  • 训练与推理速度慢（需多步迭代，如1000步）。
  • 计算资源需求高（内存和显存占用大）。

应用场景

• 高分辨率图像生成（如Stable Diffusion）、超分辨率、图像修复。

---

6. DDPM（去噪扩散概率模型，2020年6月）

背景

Diffusion Model的里程碑实现，通过马尔可夫链和噪声调度参数优化训练。

原理

• 噪声预测：模型直接预测添加的噪声${ϵ}_t$：
  $${ϵ}_{\theta }(x_t,t)\approx ϵ$$
• 去噪公式：
  $$x_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\sqrt{1-{\alpha }_t}{ϵ}_{\theta }(x_t,t)\right)$$

网络结构

• U-Net：编码器-解码器结构，处理多尺度特征。
• 时间嵌入：扩散步数$t$经正弦嵌入后输入网络。

优缺点

• 优点：
  • 理论严谨，支持灵活调度噪声参数。
  • 生成质量接近真实数据分布。
• 缺点：
  • 采样步骤多（通常需1000步），计算成本高。
  • 需要大量训练数据。

应用场景

• 图像生成（如DDPM的变体）、文本到图像（如DALLE-2）、视频生成。

---

7. Diffusion Models Beat GANs（2021年5月）

背景

通过改进扩散模型架构（如引入注意力机制），在ImageNet等数据集上超越GAN的生成质量与多样性。

关键改进

• 层次化扩散过程：分阶段处理不同尺度特征。
• 条件生成：结合文本或标签条件，增强可控性。
• 注意力机制：增强跨区域特征关联（如Transformer模块）。

原理

• 多尺度扩散：在不同分辨率下执行扩散过程，提升细节质量。
• 混合模型：结合扩散模型与GAN的判别器进行联合训练。

优缺点

• 优点：
  • 生成多样性与保真度并存，无模式崩溃。
  • 支持复杂条件生成（如文本描述生成图像）。
• 缺点：
  • 计算资源需求高，训练复杂度大。
  • 需要大量标注数据。

应用场景

• 高质量图像生成、风格迁移、艺术创作。

---

8. DALLE-2（2022年4月）

背景

结合文本到图像生成与扩散模型，通过CLIP对齐文本与视觉特征。

原理

• 文本编码器：将文本映射为CLIP的嵌入向量。
• 扩散解码器：在潜在空间（如VQ-VAE的码本）中执行扩散，逐步去噪生成图像。

网络结构

• 文本编码器：基于Transformer的编码器，输出文本嵌入。
• 扩散模型：在潜在空间中执行，使用U-Net预测噪声。
• CLIP对齐：通过对比学习对齐文本和图像的嵌入空间。

优缺点

• 优点：
  • 文本-图像对齐度高，支持复杂描述（如“一只戴帽子的熊猫在跳舞”）。
  • 生成多样性与质量平衡。
• 缺点：
  • 依赖预训练CLIP模型，计算成本高。
  • 需要大量文本-图像配对数据。

应用场景

• 文本生成图像（如MidJourney）、艺术创作、内容生成（如广告设计）。

---

9. Latent Diffusion Model（潜在扩散模型，2022年7月）

背景

在潜在空间（如VQ-VAE的离散码本）中执行扩散过程，大幅减少计算量。

原理

• 潜在空间扩散：在低维潜在空间（如$z\in {\mathbb{R}}^d$）中进行扩散，而非像素空间。
• 解码器：将潜在空间的生成结果映射回像素空间。

网络结构

• 编码器-解码器：如VQ-VAE或AutoEncoder，将图像压缩到潜在空间。
• 扩散过程：在潜在空间中执行，使用U-Net预测噪声。

优缺点

• 优点：
  • 推理速度加快（维度降低，如从$256\times 256$像素到$32\times 32$潜在码本）。
  • 生成质量与原始模型相当。
• 缺点：
  • 依赖潜在空间编码器的质量。
  • 需要额外训练编码器-解码器。

应用场景

• 高效图像生成（如Stable Diffusion）、编辑工具（如图像修复）。

---

10. UNet（2015年）

背景

由Olaf Ronneberger提出，最初用于医学图像分割，现广泛用于扩散模型的去噪网络。

原理

• 编码器（收缩路径）：卷积层提取特征，池化降低分辨率。
• 解码器（扩张路径）：反卷积恢复分辨率，跳跃连接融合多尺度特征。

网络结构

• 跳跃连接：编码器层与解码器对应层的特征拼接。
• 时间嵌入：扩散模型中需输入当前步数$t$，通过正弦嵌入扩展维度。
• 注意力机制：部分改进版UNet（如U-Net++）引入注意力模块。

优缺点

• 优点：
  • 多尺度特征融合，适配复杂任务（如医学图像的细节重建）。
  • 模块化设计，易于扩展。
• 缺点：
  • 参数量较大，计算成本高。
  • 需要大量标注数据训练。

应用场景

• 医学图像分割（如肿瘤检测）、扩散模型去噪（如DDPM、Stable Diffusion）、语义分割。

---

11. DDIM（去噪扩散隐式模型，2020年10月）

背景

由Jonathan Ho等人提出的扩散模型改进版本，通过设计非马尔可夫链加速采样过程，显著提高扩散模型的推理效率。

原理

• 隐式采样：打破马尔可夫链约束，允许直接从$x_t$到$x_{t-s}$的跳跃：
  $$x_{t-s}=\sqrt{{\alpha }_{t-s}}\left(\frac{x_t-\sqrt{1-{\alpha }_t}{ϵ}_{\theta }(x_t,t)}{\sqrt{{\alpha }_t}}\right)+\sqrt{1-{\alpha }_{t-s}}{ϵ}_{\theta }(x_t,t)$$
• 确定性推理：可选择确定性路径（无随机性），实现可控生成：
  $$x_{t-1}=\sqrt{{\alpha }_{t-1}}\left(\frac{x_t-\sqrt{1-{\alpha }_t}{ϵ}_{\theta }(x_t,t)}{\sqrt{{\alpha }_t}}\right)+\sqrt{1-{\alpha }_{t-1}}{ϵ}_{\theta }(x_t,t)$$

网络结构

• 与DDPM相同，使用U-Net预测噪声。
• 通过调度采样步数，如从1000步减少到10-50步。

优缺点

• 优点：
  • 大幅提高采样速度（可达10-100倍）。
  • 支持确定性采样，便于插值和编辑。
• 缺点：
  • 质量略低于完整步数的DDPM。
  • 参数调整复杂，需平衡速度与质量。

应用场景

• 实时图像生成、交互式编辑工具、快速原型设计。

---

12. Transformer-based Generative Models（基于Transformer的生成模型，2021年后）

背景

将Transformer架构应用于生成模型，如VQGAN+CLIP、Imagen等，结合自注意力机制的长距离依赖建模优势。

原理

• 自回归生成：类似GPT模型，逐元素生成序列。
• 扩散Transformer：将扩散模型的U-Net替换为Transformer架构。
• 双向注意力：通过交叉注意力机制融合文本与图像特征。

网络结构

• Vision Transformer (ViT)：将图像分割为patch处理。
• 交叉注意力层：融合文本特征指导图像生成。
• 位置编码：维持序列的空间信息。

优缺点

• 优点：
  • 长距离依赖建模能力强，适合复杂场景。
  • 与大语言模型架构一致，便于多模态融合。
• 缺点：
  • 计算复杂度高，尤其是自注意力机制（$O(n^2)$）。
  • 需要大量训练数据和计算资源。

应用场景

• 高质量图像生成（如Parti、Imagen）、视频生成（如Make-A-Video）、多模态生成。

---

13. ControlNet（2023年2月）

背景

由Lvmin Zhang等人提出的条件控制框架，为扩散模型增加精确的空间控制能力，实现结构化生成。

原理

• 零卷积：使用参数初始化为零的卷积层，逐步学习条件控制信号。
• 条件分支：额外的神经网络分支处理控制信号（如边缘、姿势等）。
• 特征融合：在U-Net的各层级融合条件特征。

网络结构

• 主干网络：预训练的稳定扩散模型（freeze）。
• 控制分支：与主干网络相同结构，但专注于条件信号处理。
• 特征适配器：将条件特征映射到主干网络相容的空间。

优缺点

• 优点：
  • 精确的空间控制，支持多种条件（线稿、姿势、深度等）。
  • 保留原始模型生成能力，仅增强控制层面。
• 缺点：
  • 需要特定条件数据训练。
  • 额外内存占用，增加计算负担。

应用场景

• 精确图像编辑（如姿势引导）、草图转图像、风格迁移与保持结构。

---

总结对比表

模型	核心思想	优势与局限	典型应用
GAN	对抗训练	高质量生成，但训练不稳定	图像生成、风格迁移
AE/VAE/VQ-VAE	潜在空间建模	结构化表示，但生成模糊	数据压缩、图像修复
Diffusion Model	逐步去噪生成	高保真，但速度慢	文本到图像、超分辨率
DALLE-2	文本-图像对齐	复杂描述生成，依赖CLIP	文本生成图像
Latent Diffusion	潜在空间加速	高效生成，依赖编码器质量	快速图像生成工具
UNet	多尺度特征融合	细节保留，计算成本高	医学分割、扩散模型核心
DDIM	非马尔可夫链加速	采样快，但质量略低	实时生成、快速原型设计
Transformer	自注意力机制	多模态建模强，但计算复杂	高质量图像生成、视频生成
ControlNet	条件控制	精确控制，但需要额外资源	姿势引导、草图转图像

---

未来方向

• 效率优化：如隐式扩散模型（DDIM）加速采样，或结合神经渲染技术。
• 多模态融合：结合文本、音频等生成复杂内容（如DALLE-2的扩展）。
• 可控生成：通过条件输入（如文本、属性）精细控制生成结果。