当前位置：首页 > news >正文

【漫话机器学习系列】219.支持向量机分类器（Support Vector Classifier）

news 来源：原创 2025/4/24 8:21:03

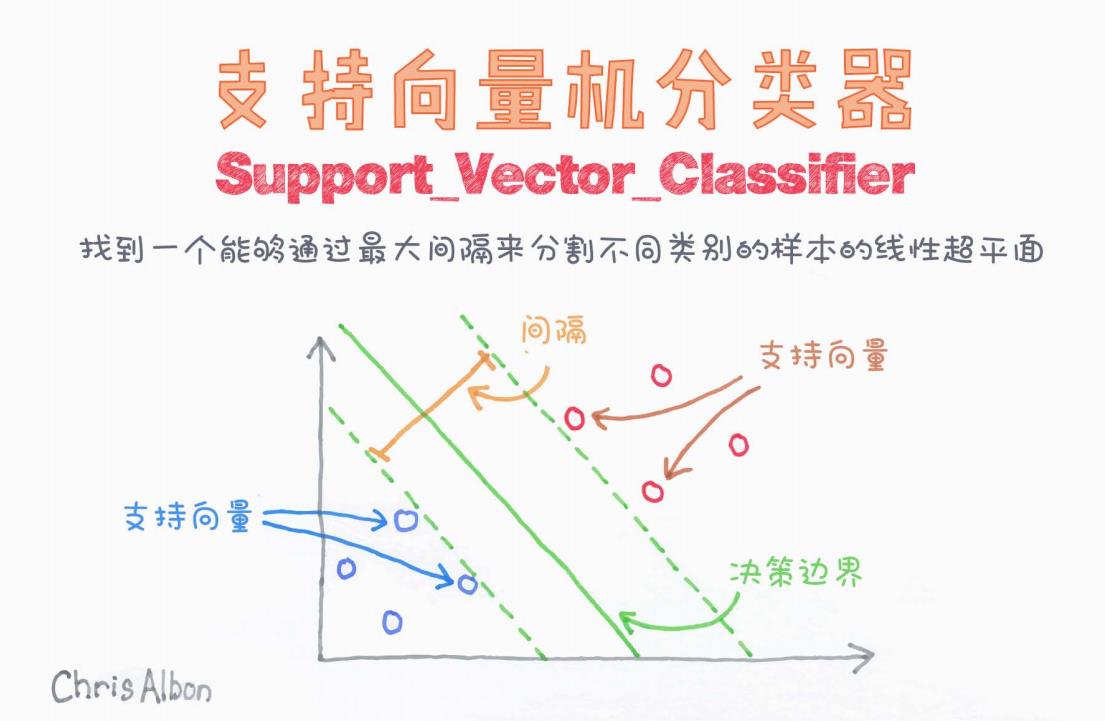
图解支持向量机分类器（Support Vector Classifier）

在机器学习的分类模型中，支持向量机（Support Vector Machine，SVM）是一种功能强大且广泛应用的监督学习算法。它尤其擅长解决小样本、高维度的数据问题，并且对结果具有较好的泛化能力。本文将结合一张手绘图，通俗而深入地讲解 SVM 中的核心概念 —— 支持向量分类器（Support Vector Classifier）。

一、什么是支持向量机分类器？

如图所示，SVM 的目标是在特征空间中找到一个最优超平面（optimal hyperplane），将不同类别的样本尽可能准确地分开。

这张图展示了二维平面上的分类情形，目标是将橙色的圆圈与蓝色的圆圈分类。

我们关注三个关键概念：

1. 决策边界（绿色实线）

这是模型最终学得的分类边界。图中显示为一条绿色实线，是我们所说的“超平面”（在二维中是直线，三维中是平面，更高维中为超平面）。

SVM 的核心思想不是仅仅找到一个可以将两个类别分开的边界，而是要找到间隔最大（Margin Maximum）的边界。

2. 间隔（Margin）（绿色虚线之间的距离）

间隔是指从决策边界到离它最近的两类样本点之间的距离。我们希望这个间隔尽可能大，也就是：

最大间隔原则：最大化到两类最近样本的距离，以提升模型泛化能力。

图中通过左右两条绿色虚线标示了间隔区域，代表模型对分类的“自信度”。

3. 支持向量（Support Vectors）

支持向量是距离决策边界最近的那些样本点。这些点“支撑”着整个超平面的位置。如果去掉这些点，分类边界的位置可能会发生改变。

图中橙色箭头指向红色圆圈（正类支持向量），蓝色箭头指向蓝色圆圈（负类支持向量），都靠近绿色的虚线边界。

这些支持向量就是模型学习的关键，因为：

决策边界由支持向量唯一决定，其余样本不会对边界产生直接影响。

二、SVM 的优化目标

从数学上来看，SVM 的本质是一个凸优化问题。假设我们有数据集 $\{ (x_i, y_i) \}$ ，其中 $y_i \in \{-1, 1\}$ ，目标是找到一个超平面 $w^T x + b = 0$ 使得：

对所有样本满足：
$y_i (w^T x_i + b) \geq 1$
同时最小化目标函数（也就是最大化间隔）：
$\min \frac{1}{2} ||w||^2$

这是一个典型的凸二次优化问题，可以通过拉格朗日乘子法、SMO（Sequential Minimal Optimization）等算法来求解。

三、软间隔与核技巧（进阶）

在现实问题中，数据往往是不可线性可分的。此时我们可以引入两个重要技术：

软间隔（Soft Margin）： 允许部分样本点可以落在间隔区域甚至被错误分类，用惩罚项 C 控制错误容忍度。
核函数（Kernel Trick）： 通过核函数将原始空间映射到高维空间，使得在高维空间中可以线性可分。常用核函数有：
- 线性核（Linear Kernel）
- 多项式核（Polynomial Kernel）
- 高斯径向基函数核（RBF Kernel）