论文学习:《聚类矩阵正则化指导的层次图池化》
原文标题:Clustering matrix regularization guided hierarchical graph pooling
原文链接:https://www.sciencedirect.com/science/article/abs/pii/S0950705125001558
图池化技术大致可以分为两类:平面图池化和层次图池化。后者通过迭代粗化来捕获图的层次结构,在各种应用中往往优于平面图池化。
平面图池化:也称为图读出函数,通过一个步骤将输入图直接映射到图级表示。
层次图池化:通过对原始图进行迭代粗化来理解其层次结构,分为节点聚类和节点丢弃技术。在节点聚类方法中,原始图的节点通过学习得到的软聚类分配矩阵进行聚类,得到的簇作为粗化图中的节点。节点丢弃技术通过学习到的打分函数计算节点得分,根据这些得分丢弃被认为不重要的节点。保留的节点被视为粗化后的图池化的节点。
信息瓶颈( Information Bottleneck,IB ):通过协调输入数据、潜在表示和目标标签之间的关系来量化表示质量,在深度学习中获得了实质性的牵引。
层次图池化可以分为两种主要的方法:节点丢弃池化和节点聚类池化,它们遵循不同的节点选择范式。
节点丢弃池化采用硬分配策略,直接丢弃被认为不太重要的节点。ASAP 提出了一种稀疏可微的池化方法,以解决捕获图子结构和确保可扩展性方面的挑战。然而,ASAP的一个显著限制是在计算节点重要性时无法显式地编码拓扑信息,这可能导致次优的池化性能。为了克服这个问题,TAPool 引入了拓扑感知池化( TAP )层,将图的拓扑结构显式地引入到节点打分中。通过将局部和全局投票得分与图连通性项相结合,TAPool可以更有效地捕获拓扑关系,提高节点选择和整体图连通性。尽管如此,节点丢弃方法固有地移除低分节点,不可避免地造成信息丢失。
节点聚类池化提供了一种软分配机制,通过聚类分配矩阵将每个节点分配到簇中,从而最小化信息损失。这些簇既作为原始图中的节点又作为粗化图中的节点,在简化图表示的同时保留了底层的结构和关系信息。
节点丢弃池化是节点聚类池化的一个具体实例,如图1所示。如果聚类矩阵的行向量被限制为one-hot向量,这种配置相当于节点丢弃池化,其中聚类分配矩阵具有最小的熵,因此包含的信息最少。这就解释了节点丢弃池化中观察到的信息损失。虽然节点聚类池化通常表现更好,但它仍然受到来自下游任务的梯度信号不足的限制,这可能导致密集学习的聚类分配矩阵包含与任务无关的噪声,从而使准确捕获节点到簇的从属关系变得更加复杂。

图1 .节点丢弃池化是节点聚类池化的一种具体形式。 节点聚类池化和节点丢弃池化可以统一在基于聚类矩阵的池化框架下。这种统一提出了一个关键的问题:如何有效地学习一个高质量的聚类矩阵来同时解决节点聚类池化中的噪声问题和节点丢弃池化中的信息丢失问题?为了增强学习结果,某些方法使用正则化损失,例如信息熵或无监督聚类损失。这些方法将聚类分配矩阵的学习过程融入先验知识,旨在细化矩阵的质量。然而,这些方法引入的先验知识通常具有较粗的粒度。虽然这些技术从经验上限制了聚类矩阵,但它们缺乏精确管理矩阵内传输信息所必需的细粒度控制。因此,矩阵中往往包含冗余的细节,可能无法服务于下游任务的特定需求,从而导致次优的结果。
为了应对这些挑战,作者坚持基于聚类矩阵的池化范式,专注于高效地学习聚类分配矩阵,其主要目标有两个:
(1)保留任务特定的信息,同时减少有用信息的丢失和最小化与任务无关的噪声;
(2)探索细粒度的学习机制,以灵活地管理矩阵内的信息传输。
层次图池化通过使用池化函数将输入图迭代地简化为更小的图,有效地捕获了层次结构信息。
(1)基于 图坍缩(Graph Coarsening)的池化机制:图坍缩是将图划分成不同的子图,然后将子图视为超级节点,从而形成一个坍缩的图。这类方法正是借用这种方式实现了对图全局信息的层次化学习。
(2)基于 TopK 的池化机制:对图中每个节点学习出一个分数,基于这个分数的排序丢弃一些低分数的节点,这类方法借鉴了CNN中最大池化操作的思路:将更重要的信息筛选出来。所不同的是,图数据中难以实现局部滑窗操作,因此需要依据分数进行全局筛选。
(3)基于 边收缩(Edge Contraction)的池化机制:边收缩是指并行地将图中的边移除,并将被移除边的两个节点合并,同时保持被移除节点的连接关系,该思路是一种通过归并操作来逐步学习图的全局信息的方法。
本文提出了一个通用的框架,利用聚类矩阵正则化来实现高质量的层次图池化(CMRGP)。CMRGP侧重于信息瓶颈中的充分性和最小化原则来定义聚类分配矩阵的理想属性。充分性保证了矩阵包含下游任务的所有必要信息,而最小化保证了它排除了多余的与任务无关的信息。在过程方面,我们首先开发了一个动态频率特征提取器,使用门控机制从节点的低频和高频信息中自适应地提取相关信息,然后生成聚类分配矩阵。该策略最大限度地减少了信息损失,提高了矩阵的充分性。然后,我们在聚类矩阵中引入噪声来创建扰动版本,以减少错误的类别隶属关系对图池化的负面影响。我们从理论上证明了引入噪声类似于压缩矩阵的信息,从而增加了矩阵的极小性。最后,我们利用扰动的聚类分配矩阵来产生一个粗化的图。考虑到聚类分配矩阵的数量与层次图池化(每层有一个矩阵)中的层数相对应,对所有矩阵施加约束可能会使模型过于复杂,并存在过拟合的风险。因此,我们对最终层的聚类分配矩阵进行了约束,并从理论上证明了该方法与替代方法是等价的。本文的贡献如下:
•分析了节点聚类池化和节点丢弃池化之间的关系,指出后者本质上是学习一个约束的聚类分配矩阵,是前者的一种特殊形式。借鉴这一思想,本文在基于聚类矩阵的层次图池化下,首次将节点聚类池化和节点丢弃池化统一起来,设定层次图池化的目标是学习一个高质量的聚类分配矩阵。
•从信息瓶颈角度分析,深入挖掘聚类矩阵内部的信息传递过程。基于这一分析,提出了一种基于聚类矩阵正则化原理的分层图池化方法CMRGP。CMRGP融合了一种动态门控机制,旨在增强聚类矩阵的可预测性,以及一种压缩聚类矩阵中不必要信息的噪声注入机制。这些特征相互配合,在聚类分配矩阵的准确性和紧凑性之间取得动态平衡。这些努力的最终结果是创建了一个预测但压缩的聚类矩阵,优化了高效的分层图池化。
提出的模型

首先,该模型以原始图Gori为输入,采用动态门控机制获取聚类分配矩阵C(0)。该矩阵同时融合了高频和低频信息,用于后续的图池化。这个过程用图中的AMP模块来说明。
接下来,我们使用C(0)对原始图Gori进行粗化。重复上述过程n次,直到产生最终的聚类矩阵Cn。
然后,模型向C(n)中注入高斯噪声对其信息进行压缩,生成最终的粗化图Gn coa,如图中POOL。
最后,我们使用一个读出函数来聚合模型产生的所有粗化的图表示。
然后将聚合的结果用于预测原始图Gori的标签Y。
1:用于计算扰动矩阵Cp和标签Y之间的互信息的信息流。
2:用于计算扰动矩阵Cp和原始图Gori之间互信息的信息流。
问题的定义和概念
在图池化中,定义图G由节点集合V= { v1,v2,..,vN }、边集合E= { e1,e2,..,eM }和节点特征矩阵X = [ x1 , x2 , ... , xN]⊤∈R N×D组成,统称为G = ( V, E, X)。每个节点和边通过邻接矩阵A∈R N×N和节点特征矩阵X的相互作用来定量描述。图池化过程使用池化函数将原始图Gori转化为粗化图Gcoa。这种转换在简化图的同时保留了语义丰富的信息,从而方便了更有效的下游任务。例如,在图分类任务中,考虑一个数据集D = { ( G1 ori , Y1),..,( Gn ori , Y n) },其中Gi ori表示第i个原始图,Yi表示与该图相关的类别标签。池化函数使用聚类矩阵C∈R N×M将D中的每个图Gi ori转化为粗化图Gi coa,其中N表示Gi ori中的节点数,M表示Gi coa中的节点数。随后,粗化后的图Gi可以经过n次池化函数的迭代,从而得到图级的表示。我们对整体过程的形式化定义如下:
输入:给定一组图{G1 ori,..,Gn ori},一组图类别标签{Y1,..,Yc},图类别数c。
输出:未知图的类别标签^Y。
目标函数:
![]()
分类采用了一个目标函数,该目标函数集成了一个分类损失Lcls来评估图标签预测对真实标签Y的准确性,以及一个正则化项Lreg来保持原始图和粗化图之间的结构完整性。该目标函数中的超参数α被微调以平衡这两个方面,同时优化了图简化的保真度和分类的准确性。
本文的目标是开发一个高质量的聚类矩阵来增强层次图池化的性能。在信息瓶颈原理的指导下,设计了如下的目标函数:
![]()
这里,I(C;Y)表示聚类分配矩阵和标签之间的互信息,与公式(1) 中的第一项对齐。此外,I(C;Gori)表示聚类矩阵与原始图之间的互信息,对应于公式(1) 式中的第二项。公式( 2 )对聚类矩阵施加约束,保证学习到的矩阵是充分且极小的。该方程旨在优化信息保持和最小化之间的平衡,促进下游任务的有效表征。在这个优化框架下,接着描述了模型的前向计算过程。
聚类矩阵生成器
在图池化过程中,从原始图中导出有效的聚类矩阵是至关重要的。由于其在各种图任务中的鲁棒性能,图神经网络( GNNs )经常被用于生成这些矩阵。然而,由于GNNs主要作为低通滤波器发挥作用,它们主要传输节点的低频信息,而忽略了高频细节。这种限制可能导致聚类矩阵缺乏重要的任务特定信息,从而潜在地破坏下游任务的有效性。为了解决这个问题,我们将高频信息融入到聚类矩阵的创建中。提出了一种动态门控机制来平衡高低频信息的传输,增强了聚类矩阵的表达能力。具体来说,我们使用归一化邻接矩阵~A和归一化拉普拉斯矩阵~L作为卷积核来动态捕获低频和高频节点信息。这些核对聚类矩阵的影响会根据图数据的变化情况而变化。该方法的形式化描述如下:

这里,C(i+1)∈R N×M表示第(i+1)层的聚类矩阵,每个元素Cij表示节点i和类别j之间的连接强度。⊙符号表示Hadamard积,W∈R D×M表示第i层的参数矩阵,λ∈R N×D表示第i层节点的原始域信息,具有可训练性。公式(3)利用更新门λ调控C在元素层面的信息传递,保证C中的每个元素同时从低频源和高频源中获得最详细的信息。我们证明了由任意一个池化层创建的聚类矩阵C,根据公式(3)整合了高频和低频信息,包含了比单独由高频或低频信息生成的聚类矩阵Chigh = ~-L(i)X(i)和Clow =^~A (i)X(i)更多的任务相关信息。相关命题如下。
命题1。给定根据式( 3 )生成的足够多的聚类矩阵C,与仅由高频或低频信息形成的矩阵Chigh和Clow相比,它拥有更多的任务相关信息。这一过程记为:

证明。利用深度学习中常用的马尔可夫链假设证明了该命题。在模型中,马尔科夫链定义为

利用数据处理不等式(DPI),我们建立了这个Markov链
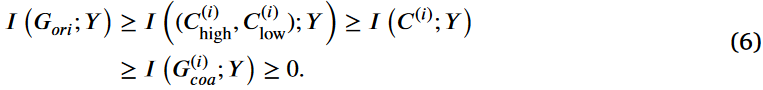
随后,由于C(i)是充分的,则有
![]()
通过整合(5)和(6),Markov链中的一些变量被证明是充分的,即,

利用互信息的链式规则,我们分解C(i) high,C(i) low和标签Y之间的联合互信息来寻找

最终,我们得到I(C(i);Y )≥I (C(i)high;Y )和I(C(i);Y )≥I ( C(i)low;Y )由式(9)可得,从而完成证明。
命题1表明,由式( 3 )生成的聚类矩阵C比仅集成高频信息的矩阵Chigh和仅集成低频信息的矩阵Clow捕获了更多的下游任务相关信息,表现出更强的充分性。这一观察与直觉预期一致,即在模型中其他地方不变的条件下,处理多视图数据输入的模型通常优于仅限于单视图输入的模型。原因在于多视图数据包含了更广泛的任务相关信息。因此,最大化输入到模型中的任务相关信息是可取的。增强原始数据或集成多样化的辅助数据源可以有效地实现这一点,从而优化复杂任务的模型性能。
压缩信息的噪声注入
一旦得到来自第i层的聚类矩阵C(i),目标是消除与下游任务无关的信息。本文在C(i)中引入受控噪声,形成一个扰动矩阵C(i) p 。这种噪声注入的目的不是增加固有噪声,而是对矩阵进行正则化,通过帮助模型区分有意义和虚假的节点类从属关系来增强模型的鲁棒性。虽然噪声可能最初扰乱数据分布,并似乎阻碍了有价值的信息传输,但当适当应用时,它有效地创建了信息瓶颈。该瓶颈调节C(i)和C(i) p之间的信息流动,选择性地传递有用信息并过滤掉不相关的数据,如图3所示。通过这种方式,模型不仅维护而且关注下游任务所需的关键数据。从信息论的角度来看,适当地引入噪声有助于获得最小版本的C(i) p,并针对手头的任务进行优化。

向聚类矩阵C(i)中注入噪声的过程开始于选择一个独立的多元高斯噪声ε∈RNM × 1~N( μ∈RNM × 1 , σ∈RNM × NM),其中μ = 1是所有均值都等于1的向量,σ是定义为σ = E [(ε - μ)(ε - μ)T]的对角协方差矩阵。设置所有的均值为1,确保扰动后的聚类关系的期望值E (C(i) p)与原始矩阵的期望值C(i)保持一致。为了在训练过程中确保可区分性并启用反向传播,采用了重新参数化技巧。具体来说,高斯噪声ε被重新参数化为:
![]()
式中:γ⋅(0 , I)表示标准正态随机变量,σ = fσ(C(i))表示可学习的标准差,确保噪声既可控又能适应各种数据集。方差σ使用ReLU激活的神经网络来确定,以确保非负性,表示为:
![]()
其中Wσ表示神经网络的可学习权重。扰动聚类矩阵C(i) p由采样噪声ε与聚类矩阵C(i)按元素相乘得到,其形式为:
![]()
这种受控的噪声注入产生了一个信息瓶颈,通过限制与任务无关的信息的传输来规则化聚类矩阵。
式( 12 )中,聚类矩阵C(i)∈RN × M被认为是一个维数为NM的向量。其中,N表示输入图中的节点数,M表示对应的粗化图中的节点数。给定向量C(i),C(i) p的条件分布记为p(C(i) p|C(i))~N(C(i),M(i)⊙σ)。这里矩阵M(i)∈RNM × NM定义为
![]()
在训练过程中,如果C(i)中节点i与类别j之间的关系Cij是真实的,则相应的噪声εij对Cij的影响会逐渐减小,收敛于1。反之,若Cij发生扭曲,则噪声εij的强度会加剧,显著偏离1。这一行为表明噪声向量ε可以有效地过滤C(i)中的真实关系。理论上,我们证明了注入噪声压缩了扰动聚类矩阵C(i) p中的信息。我们为C(i) p和C(i)之间的互信息I(C(i),C(i) p)提供了一个实用的上界,确保模型只保留最相关的信息。该方法的理论基础和含义在下面提出的相应命题中进行了阐述。
命题2。对于一个已注入噪声ε的扰动聚类矩阵C(i) p,C(i)能够传递给C(i) p的信息量存在一个上界,形式表示为:

证明。通过计算互信息I (C(i);C(i) p)介于C(i)和C(i) p之间,故确定C(i) p
![]()
当指定C(i)时,C(i) p的条件概率为p(C(i) p|C(i))⋅(C(i),M(i)⊙σ )。依此设定,应用高斯分布的熵公式计算C(i) p的条件熵为
![]()
这里det是指C(i) p的协方差矩阵的行列式。NM表示C(i) p的维数,反映了该矩阵的复杂程度。考虑到引入的噪声ε的分量是独立的,p(C(i) p|C(i))也被认为是独立的。因此,协方差矩阵ΣC(i) p|C(i)是对角的,其行列式通过沿对角线的元素相乘来计算。由于ΣC(i) p|C(i)是由C(i)定义的确定性函数,一旦指定了C(i),它就变得显式已知。利用总期望E(C(i) p) = EC(i)[E(C(i) p|C(i))]和总方差Var(C(i) p) = EC(i)[Var(C(i) p|C(i))] + Var[E(C(i) p|C(i))]的规律,可以得到C(i) p的期望和协方差分别为E(C(i)p) = E(C(i))和Var(C(i) p) = σ⊙[Var(C(i)) + E(C(i))E(C(i))T] 。给定均值向量E(C(i) p)和协方差矩阵Var(C(i) p),C(i) p的最大熵分布为ME (p(C(i) p))~N(E(C(i) p),Var(C(i) p)),其中 (C(i) p)的上界为
![]()
最后,这个框架允许建立I(C(i)的一个上界;C(i) p)为

命题2表明,在注入适当的高斯噪声后,聚类矩阵C(i)与其扰动对应物C(i) p之间的互信息是有限的,从而产生了一个可控的上界。这意味着通过降低这个上界,我们可以减少从C(i)到C(i) p的信息流,从而降低模型中过拟合的风险。
图粗化
一旦获得来自第i层的扰动聚类矩阵C(i) p,C(i) p中的节点和类别之间的隶属关系被应用于节点和边特征以产生粗化图。这种转换被形式化为:

其中,Xi表示节点特征,Al表示粗化图的邻接矩阵。
模型优化
在(2)中,I(C ; Y)和I(Gori; C)分别表示聚类矩阵C和标签Y之间以及原始图G和聚类矩阵C之间的互信息。这些度量在层次图池化中至关重要,它涉及多次粗化图的迭代来阐明其层次结构,并在此过程中产生若干聚类矩阵。为了优化计算效率,我们选择只在最终的聚类矩阵C(n)中注入噪声,而不是序列中的每个矩阵。该决策在不影响模型完整性的前提下,减少了计算开销。得到的扰动聚类矩阵记为C(n) p,然后用其代替C(n)。这种修改以信息瓶颈原理为指导,旨在通过有效地控制信息的流动,最大限度地减少信息冗余。为了适应这些变化,我们相应地调整我们的目标函数,现在定义为
![]()
考虑到我们的目的是优化这些互信息而不是精确地计算它们,我们建立了一个可管理的下界为I(C(n) p;Y)和上界为I(Gori;C(n) p),以方便实际应用。最大化I (C(n) p;Y)增强了C(n) p中关于Y的信息,这意味着将C(n) p中的节点-类别从属关系与标签紧密对齐。直接优化I(C(n) p;Y)由于其计算复杂性而提出了挑战,因此我们设定了一个可行的下界为I(C(n) p;Y)

与现有方法的区别
(1)层次图池化的统一框架。本文的研究是第一个在基于单个聚类矩阵的范式下统一节点聚类池化和节点丢弃池化的研究。本文从信息论的角度将节点丢弃池化解释为节点聚类池化的受限变体,这一见解提供了对层次图池化的更广泛的理解,为未来探索基于聚类矩阵的方法奠定了基础。
(2)聚类分配矩阵中的信息瓶颈视角。本文提出利用信息瓶颈原理来分析和指导聚类分配矩阵的学习。与现有的应用粗粒度正则化损失的方法不同,采用细粒度信息控制,引入充分性和最小化作为补充目标。这种视角使得学习既具有预测性又具有紧凑性的聚类矩阵成为可能,这比传统方法往往忽略这些属性之间的平衡迈出了一步。
(3)动态门控和噪声注入机制。本文引入创新机制来解决聚类分配矩阵中噪声和信息丢失的挑战。动态门控机制同时适应低频和高频特征,保证了任务相关信息的保留。同时,噪声注入机制压缩了无关信息,有效地提高了聚类矩阵的质量。这种双重方法是对缺乏这种细致入微控制的传统方法的实际推进。
