Java实现加密（七）国密SM2算法的签名和验签（附商用密码检测相关国家标准/国密标准下载）

一、国密标准中，关于SM2签名验签的定义

参考 《GM∕T 0003-2010 SM2椭圆曲线公钥密码算法.pdf》

其中第2部分对于数字签名的描述如下：

• 数字签名算法 由一个 签名者 对数据产生数字签名，并由一个 验证者 验证签名的可靠性。每个签名都有一个公钥和私钥，其中私钥用于产生签名，验证者用签名者的公钥验证签名。

标准原始描述截图如下：

补充：《SM2椭圆曲线公钥密码算法》共分为四个部分：

• 第1部分：总则
• 第2部分：数字签名算法
• 第3部分：密钥交换协议
• 第4部分：公钥加密算法

注意：在 SM2 算法中涉及的公钥、私钥、签名的长度基本是固定的，以下为标准长度，可以比对参考长度是否争取：

标准公钥：
23BCB208E10056523D4F4090C0130D5B8898A858E8D5D9FF3B16572FA04E70E28A88459060FF5D88CC53D77407619F9B8B584317A30EDDFCA71DC4965F3ED143

标准私钥：
CBD981B9C2FC49D9E497A68EB4EA3AC2E33472CCECBA7EA803B1A1DDB3B0EBCE

标准签名数据：
R：D00C1DEFEAD263A0FEDDE0AEC26274DBB80719385BB3DDD9AB2A31FB11F378C3

R：00CE562BE2CEB0DDD0DD18E925FF00AB87BB67BB33F4234967F82EDC3798265CDF

S：F1BEDD87A2B17D7150E4ECDCFAEB0D3E34AFE5985CB4EFA39D4FDCE7B32CFBE4

在线网址：
SM2 密钥在线生成工具：https://const.net.cn/tool/sm2/genkey/
SM2 在线签名生成工具（带userId）：https://const.net.cn/tool/sm2/sign/
SM2 在线验签工具（带userId）：https://const.net.cn/tool/sm2/verify/

---

二、SM2签名和验签的实现原理

1. 前置知识

• 椭圆曲线参数：
  SM2 使用特定的椭圆曲线方程（如 y^2 = x^3 + ax + b ）和公开参数：
  • 基点 G（生成元）。
  • 阶 n（基点的阶，一个大素数）。
• 密钥对：
  • 私钥 d：随机数，1 ≤ d ≤ n−1。
  • 公钥 P：椭圆曲线上的点，P = d ⋅ G。
• 哈希函数：
  SM3 算法（国密标准哈希函数），用于计算消息和用户ID的哈希值。

---

2. 签名生成过程

签名者对消息 M 生成签名 (r,s)，步骤如下：

步骤 1：计算哈希值 ZA 和 e

• 用户ID哈希（ZA）：
  将用户ID（如身份证号、邮箱等）与公钥绑定，防止身份伪造：

  $$ZA=\text{SM3}(\text{UserID}\parallel \text{公钥坐标}\parallel \text{曲线参数})$$

• 消息哈希（e）：
  结合 ZA​ 和原始消息 M：

  $$e=\text{SM3}(ZA\parallel M)$$

步骤 2：生成随机数 k

• 随机选择 k∈[1,n−1]，且每次签名必须不同（否则私钥会泄露）。

步骤 3：计算临时椭圆曲线点 (x1, y1)

$$(x_1,y_1)=k\cdot G$$

• 取 x1 的整数形式，计算 r ：

  $$r=(e+x_1)\mathrm{mod}n$$

  若 r=0 或 r+k=n，需重新选择 k。

**步骤 4：计算签名值 s

$$s=(1+d{)}^{-1}\cdot (k-r\cdot d)\mathrm{mod}n$$

• (1+d)−1 是模 n 下的乘法逆元。
• 若 s=0，需重新签名。

最终签名

输出 (r,s) 作为数字签名（通常编码为 64 字节，r 和 s 各 32 字节）。

---

3. 验签过程

验签者使用公钥 P 验证签名 (r, s) 的合法性：

步骤 1：检查 r 和 s 范围

• 确保 r, s∈[1, n−1]，否则验签失败。

步骤 2：重新计算哈希值 e

• 使用相同的 UserID 和公钥计算 ZA 和 e（与签名过程一致）。

步骤 3：计算中间值 t

$$t=(r+s)\mathrm{mod}n$$

• 若 t=0，验签失败。

步骤 4：恢复临时点 (x1, y1)

$$(x_1,y_1)=s\cdot G+t\cdot P$$

• 利用公钥 P=d⋅G，推导如下：

  $$s\cdot G+t\cdot P=s\cdot G+t\cdot d\cdot P=(s+t\cdot d)\cdot G$$

  • 签名时：

    $$s\equiv (1+d{)}^{-1}\cdot (k-rd)\mathrm{mod}n$$

    ，代入可得：

    $$s+t\cdot d\equiv k\mathrm{mod}n$$

  • 因此恢复的点应为 k ⋅ G，即签名时的 (x1, y1)。

步骤 5：验证 r 的合法性

$$R=(e+x_1)\mathrm{mod}n$$

• 检查是否满足 R = r ：
  • 若成立，验签通过；否则失败。

---

4. 数学正确性证明

验签的关键在于通过公钥 P 和签名 (r, s) 重构出签名时的临时点 k⋅G ：

1. 签名时：

   $$s\equiv (1+d{)}^{-1}(k-rd)\mathrm{mod}n$$

2. 两边乘 (1+d) 得：

   $$s(1+d)\equiv k-rd\mathrm{mod}n$$

3. 整理后：

   $$k\equiv s+(s+r)d\mathrm{mod}n$$

   • 注意到 t = r + s，故 k ≡ s + td mod n。

4. 验签时计算的点：

   $$s\cdot G+t\cdot P=(s+td)\cdot G=k\cdot G$$

   • 与签名时的 (x1, y1) 一致，确保 x₁ 匹配。

---

5. 安全性与注意事项

1. 随机数 k 的安全性：
   • k 必须不可预测且不重复，否则攻击者可通过两次签名反推私钥（类似 ECDSA 的漏洞）。
2. UserID 的作用：
   • 绑定用户身份与公钥，防止公钥替换攻击。
3. 哈希函数：
   • 必须使用 SM3 算法，确保与国密标准兼容。
4. 抵抗攻击：
   • 基于椭圆曲线离散对数问题（ECDLP）的困难性，无法从 P=d⋅G 推导出 d。

---

三、带userId、不带userId的区别

SM2的签名验签分为带userId和不带userId两种，主要是根据签名验签时是否需要userId作为入参来进行区分。

• 带 UserID：
  多一步预处理（计算 ZA），将用户身份、公钥和曲线参数绑定到哈希中，形成身份感知的签名。
• 不带 UserID：
  跳过预处理，仅哈希原始消息，签名仅依赖公钥和消息本身。

1. 核心区别

特性	带 UserID 的 SM2	不带 UserID 的 SM2
哈希输入	计算 `ZA = SM3(UserID
身份绑定	签名与特定用户身份（UserID）强绑定	仅绑定公钥和消息，无用户身份信息
安全性	防止公钥替换攻击（需伪造 UserID）	仅依赖公钥，易受公钥替换攻击
国密标准合规性	✅符合 GM/T 0003-2012 标准	❌非标准用法，通常不推荐

2.算法区别

(1) 哈希计算过程

• 带 UserID：

  1. 先计算 ZA（用户身份哈希）：

     $$ZA=\text{SM3}(\text{UserID}\parallel \text{公钥坐标}\parallel \text{曲线参数})$$

  2. 再计算消息哈希 e：

     $$e=\text{SM3}(ZA\parallel M)$$

  • 作用：将用户身份、公钥和消息绑定，确保签名无法被其他用户复用。

• 不带 UserID：
  直接计算消息哈希：

  $$e=\text{SM3}(ZA\parallel M)$$

  • 风险：攻击者可替换公钥，伪造签名（缺乏身份绑定）。

(2) 签名验签流程

• 带 UserID：

  • 签名：

    $$r=(e+x_1)\mathrm{mod}n(x_1来自k\cdot G)$$

    $$s=(1+d{)}^{-1}\cdot (k-r\cdot d)\mathrm{mod}n$$

  • 验签：
    验签方需使用相同的 UserID 重新计算 ZA 和 e，否则验签失败。

• 不带 UserID：
  跳过 ZA 计算，直接使用 e = SM3(M)，其余步骤相同。

---

四、Java代码实现

1. Maven 依赖

<!-- BC库 -->
<dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15on</artifactId><version>1.70</version>
</dependency>

2. 代码实现

SM2WithUserIdExample.java

import org.bouncycastle.crypto.params.ECDomainParameters;
import org.bouncycastle.crypto.params.ECPrivateKeyParameters;
import org.bouncycastle.crypto.params.ECPublicKeyParameters;
import org.bouncycastle.crypto.params.ParametersWithID;
import org.bouncycastle.crypto.signers.SM2Signer;
import org.bouncycastle.jce.ECNamedCurveTable;
import org.bouncycastle.jce.provider.BouncyCastleProvider;
import org.bouncycastle.jce.spec.ECNamedCurveParameterSpec;
import org.bouncycastle.util.encoders.Hex;import java.security.*;public class SM2WithUserIdExample {static {Security.addProvider(new BouncyCastleProvider());}// SM2曲线参数private static final ECNamedCurveParameterSpec SM2_SPEC = ECNamedCurveTable.getParameterSpec("sm2p256v1");public static void main(String[] args) throws Exception {// 生成SM2密钥对KeyPair keyPair = generateSM2KeyPair();System.out.println("Public Key: " + Hex.toHexString(keyPair.getPublic().getEncoded()));System.out.println("Private Key: " + Hex.toHexString(keyPair.getPrivate().getEncoded()));// 用户IDbyte[] userId = "1234567812345678".getBytes();// 待签名的消息String message = "Hello, SM2!";// 使用用户ID进行签名byte[] signature = signWithUserId(keyPair.getPrivate(), userId, message.getBytes());System.out.println("Signature: " + Hex.toHexString(signature));// 使用用户ID进行验签boolean isValid = verifyWithUserId(keyPair.getPublic(), userId, message.getBytes(), signature);System.out.println("Signature valid: " + isValid);}// 生成SM2密钥对public static KeyPair generateSM2KeyPair() throws Exception {KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("EC", "BC");keyPairGenerator.initialize(SM2_SPEC, new SecureRandom());return keyPairGenerator.generateKeyPair();}// 使用用户ID进行签名public static byte[] signWithUserId(PrivateKey privateKey, byte[] userId, byte[] message) throws Exception {ECPrivateKeyParameters privKey = new ECPrivateKeyParameters(((java.security.interfaces.ECPrivateKey) privateKey).getS(),new ECDomainParameters(SM2_SPEC.getCurve(), SM2_SPEC.getG(), SM2_SPEC.getN()));SM2Signer signer = new SM2Signer();signer.init(true, new ParametersWithID(privKey, userId));signer.update(message, 0, message.length);return signer.generateSignature();}// 使用用户ID进行验签public static boolean verifyWithUserId(PublicKey publicKey, byte[] userId, byte[] message, byte[] signature) throws Exception {java.security.spec.ECPoint publicPoint = ((java.security.interfaces.ECPublicKey) publicKey).getW();org.bouncycastle.math.ec.ECPoint bcPublicPoint = SM2_SPEC.getCurve().createPoint(publicPoint.getAffineX(),publicPoint.getAffineY());ECPublicKeyParameters pubKey = new ECPublicKeyParameters(bcPublicPoint,new ECDomainParameters(SM2_SPEC.getCurve(), SM2_SPEC.getG(), SM2_SPEC.getN()));SM2Signer verifier = new SM2Signer();verifier.init(false, new ParametersWithID(pubKey, userId));verifier.update(message, 0, message.length);return verifier.verifySignature(signature);}
}

3. 测试结果

Public Key: 04d1a1065f36c116040a5aef12c2f9f34fd26a0af4e639f6602f9ad252fdaddcbe62bb4c7e065b6391822ec56e6822baded04bd98cf909a846e4a17b61cc9ae7de
Private Key: 308193020100301306072a8648ce3d020106082a811ccf5501822d047930770201010420c9e443b10c9f567cfa014f2982a307bf5473612540fc597a1bffa4be8f277b9ca00a06082a811ccf5501822da14403420004d1a1065f36c116040a5aef12c2f9f34fd26a0af4e639f6602f9ad252fdaddcbe62bb4c7e065b6391822ec56e6822baded04bd98cf909a846e4a17b61cc9ae7de
Message: 48656c6c6f2c20534d3221
Signature: 3046022100a3a8ed43fd20d85edfc72744eebf58a205b8c92e87dd7c286770f2e9f22aee68022100fcab418b2961cce41f514fe1851d85266cef66cf5178201778b570e8eebb8d9f
Signature valid: true

4. 签名结果解析R和S

签名内容实际是16进制ASN.1格式的字节流，我们可以使用工具网站进行在线解析。

• 解析网站： https://the-x.cn/zh-cn/encodings/Asn1.aspx

解析结果如下：

• R：A3A8ED43FD20D85EDFC72744EEBF58A205B8C92E87DD7C286770F2E9F22AEE68
• S：FCAB418B2961CCE41F514FE1851D85266CEF66CF5178201778B570E8EEBB8D9F

5. 在线验证

• 验证网址： https://const.net.cn/tool/sm2/verify/

我们将对应的公钥、原文、签名（R+S）按照十六进制格式输入之后就可以成功验证了。

注意：

1.公钥信息需要去除04前缀；
2.原文不要直接输入，需要转换为十六进制；
3.签名的R、S需要去除00前缀。

如果验证结果为空，页面会展示具体的报错原因，在如下图所示的位置：

（例如公钥没有去除 04 前缀时的报错）

---

五、签名的ASN.1结构解析

我们将上一步代码生成示例的原签名和解析后的 R、S 进行拆分比对：

可以发现签名的拼接规律如下：

完整签名=3046+022100+R+022100+S

看到这里，恭喜你！你已经发现了ASN.1结构的规律！

1. ASN.1整体结构

SM2 签名默认输出为 DER 编码的 ASN.1 格式，包含两个整数 r 和 s。完整编码结构如下：

SEQUENCE (30) → 包含两个 INTEGER (02)│├── INTEGER (02) → r└── INTEGER (02) → s

2. 字段解析

以 3046022100...022100... 为例：

字节位置	值（Hex）	含义
0-1	30	SEQUENCE 标签，表示后续是一个结构体。
2	46	SEQUENCE 长度，表示后续 70 字节（0x46 = 70）是序列内容。
3-5	022100	INTEGER 标签和长度，表示 r 是一个 32 字节（0x21 = 33，含前缀 00）的正整数。
6-37	...	r 的具体值（32 字节）。
38-40	022100	INTEGER 标签和长度，表示 s 是一个 32 字节的正整数。
41-72	...	s 的具体值（32 字节）。

3. 关键字段说明

1) 3046

• 30：ASN.1 的 SEQUENCE 标签（表示复合结构）。
• 46：序列的 总长度（70 字节），计算如下：
  • r 部分：02（标签） + 21（长度） + 00（前缀） + 32 字节 = 35 字节。
  • s 部分：同上，35 字节。
  • 总计：35 + 35 = 70 字节 → 0x46。

2) 022100

• 02：ASN.1 的 INTEGER 标签。
• 21：整数的长度（33 字节，包含前缀 00）。
• 00：前缀字节（因 r/s 的最高位为 1，需补 00 避免被当作负数）。

4. 为什么需要 00 前缀？

• 规则：若整数的最高位（MSB）为 1，需补 00 避免被误认为是负数（ASN.1 的 INTEGER 是带符号的）。
• 示例：
  • 若 r 的第一个字节是 0x8F（二进制 10001111），需补 00 变为 008F...。
  • 若 r 的第一个字节是 0x3F（二进制 00111111），无需补 00。

5. 实际签名示例

假设签名值为：

3046022100A1B2C3...（32字节）022100D4E5F6...（32字节）

• 解析：
  • 30 46：SEQUENCE，长度 70 字节。
  • 02 21 00：r 是 33 字节（含前缀 00），实际值 32 字节。
  • A1B2C3...：r 的具体数据。
  • 02 21 00：s 是 33 字节（含前缀 00），实际值 32 字节。
  • D4E5F6...：s 的具体数据。

---

6. 代码验证（Java + Bouncy Castle）

import org.bouncycastle.asn1.ASN1Sequence;
import org.bouncycastle.asn1.DERSequence;
import org.bouncycastle.util.encoders.Hex;public class SM2SignatureParser {public static void main(String[] args) {String derSignature = "3046022100A1B2C3...022100D4E5F6..."; // 示例签名byte[] signatureBytes = Hex.decode(derSignature);// 解析 DER 编码ASN1Sequence sequence = ASN1Sequence.getInstance(signatureBytes);BigInteger r = ((ASN1Integer) sequence.getObjectAt(0)).getValue();BigInteger s = ((ASN1Integer) sequence.getObjectAt(1)).getValue();System.out.println("r: " + r.toString(16));System.out.println("s: " + s.toString(16));}
}

---

五、补充：商用密码检测相关标准下载

1. GB/T 15843 国家标准（权限鉴别相关）

15843标准共分为6部分，第1部分为总则。

《GB∕T 15843.1-2017 信息技术　安全技术　实体鉴别　第1部分：总则.pdf》
《GB∕T 15843.2-2024 网络安全技术 实体鉴别 第2部分：采用鉴别式加密的机制.pdf》
《GB∕T 15843.3-2023 信息技术 安全技术 实体鉴别 第3部分：采用数字签名技术的机制.pdf》
《GB∕T 15843.4-2024 网络安全技术 实体鉴别 第4部分：采用密码校验函数的机制.pdf》
《GB∕T 15843.5-2005 信息技术　安全技术　实体鉴别　第5部分：使用零知识技术的机制.pdf》
《GB∕T 15843.6-2018 信息技术 安全技术 实体鉴别 第6部分：采用人工数据传递的机制.pdf》

下载地址： https://share.weiyun.com/bEAhW1Ec

如果只是为了检测时满足国家标准，最简单地可以参考第2部分的单次鉴别。

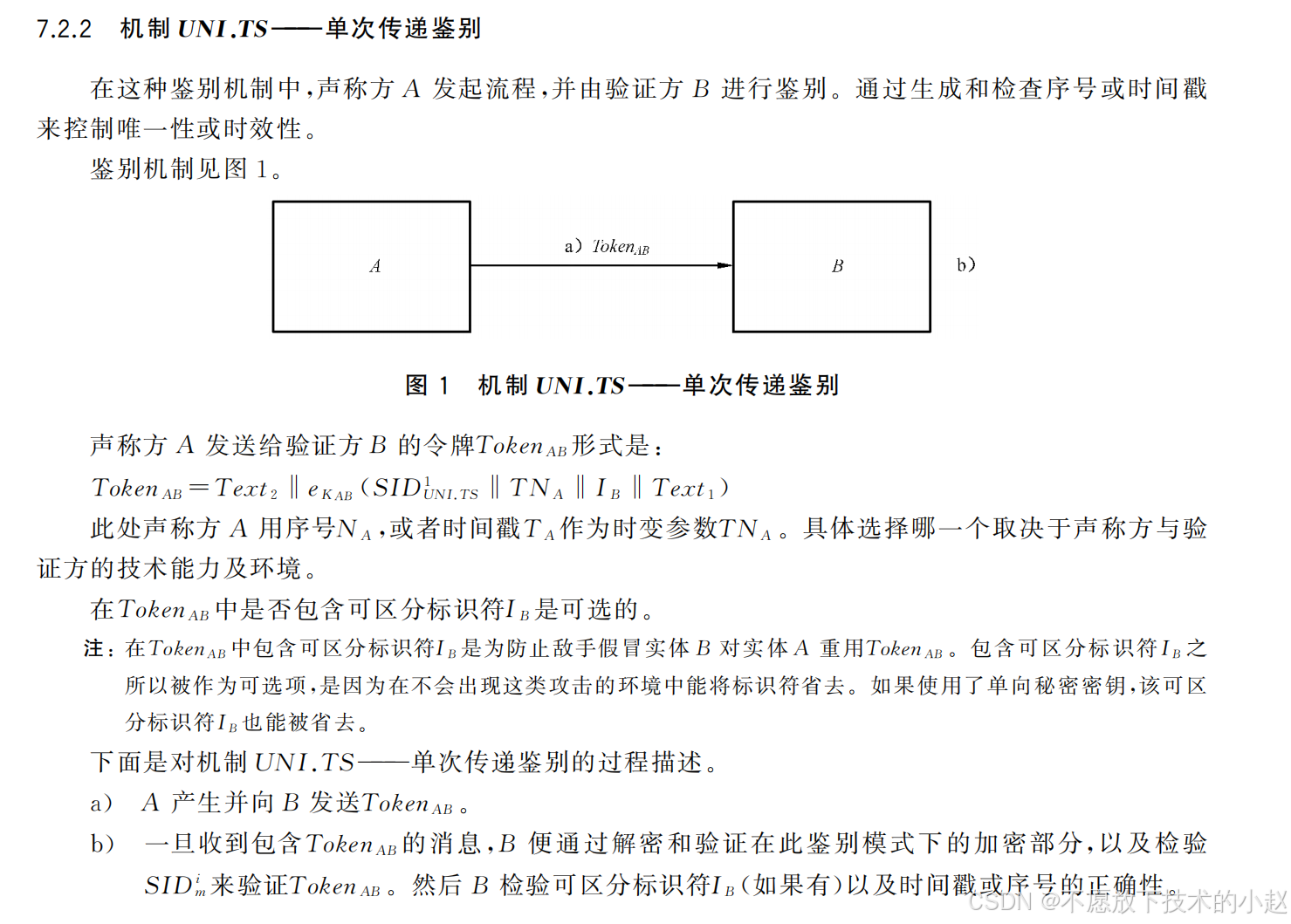
2. GB/T 38540国家标准（电子 签章相关，参考）

《GB∕T 38540-2020 信息安全技术 安全电子签章密码技术规范.pdf》

下载地址： https://share.weiyun.com/Mw2EwyZl

3. GM/T 0003 国密标准（SM2算法）

《GM∕T 0003-2010 SM2椭圆曲线公钥密码算法.pdf》

下载地址： https://share.weiyun.com/PvwgP2sM

4. GM/T 0031国密标准（电子签章相关，参考）

《GMT 0031-2014 安全电子签章密码技术规范.pdf》

下载地址： https://share.weiyun.com/VA5zlwVW

5.其余国家标准下载

全国网络安全标准化技术委员会：https://www.tc260.org.cn/front/bzcx/yfgbcx.html

（该地址可以下载国家标准文件，但是仅供参考，部分国家标准搜索不到。）

6. 其余国密标准下载

区别于国家标准有版权限制，国密标准可以直接在官方网站进行下载。

国家密码管理局-官网地址： https://www.oscca.gov.cn/sca/index.shtml

例如，我们下载SM3标准，可以先进行搜索，如下所示：

搜索之后可以看到下面有相关的文件，点击就可以直接下载了。

7. GB/T 38540 国家标准和 GM/T 0031 国密标准的应用场景差异：

场景	GB/T 38540适用性	GM/T 0031适用性
国际化业务（如跨境电子合同）	✅ 优先采用	❌ 不适用
政府/金融等关键领域	可选	✅ 强制符合
商用密码产品认证	❌ 无法用于过密评	✅ 必需符合

整理完毕，完结撒花~🌻

参考地址：

1.SM2 签名验签 注意事项，https://blog.csdn.net/softt/article/details/141570577