神经网络与深度学习第四章-前馈神经网络

前馈神经网络

在本章中，我们主要关注采用误差反向传播来进行学习的神经网络。

4.1 神经元

神经元是构成神经网络的基本单元。主要是模拟生物神经元的结构和特性，接收一组输入信号并产生输出。
现代神经元中的激活函数通常要求是连续可导的函数。

净输入代表了输入信号对神经元的总和刺激强度，是激活函数的输入值。 净输入可以：①决定神经是否激活；②反映输入信号的整合效果。

激活函数。为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：
（1）连续且可导（允许在少数点上不可导）的非线性函数。可导的激活函数可以直接利用数值优化的方法（比如梯度下降法）来学习网络参数。
（2）激活函数及其导函数尽可能简单，可以提高网络计算效率。
（3）激活函数的导函数的值域要在一个合适的区间内，否则会影响训练的效率和稳定性。

4.1.1 Sigmoid型函数

Sigmoid型函数是指一类S型曲线函数，是两端饱和函数。常用的该类型函数是Logistic函数和Tanh函数。

对于函数 f(x) ,若x -> 负无穷 时，其导函数 f'(x)->0,则称其为左饱和；若x -> 正无穷 时，其导函数 f'(x)->0,则称其为右饱和；当同时满足左右饱和时，称为两端饱和。

Logistic函数类似于一个“挤压”函数，把一个实数域的输入“挤压”导（0，1）。
当输入值在0附近时，Sigmoid型函数近似于线性函数；
当输入值靠近两端时，对输入进行抑制。输入越小，越接近于0；输入越大，越接近于1.

和感知器使用的阶跃激活函数相比，Logistic函数是连续可导的，数学性质更好。

所以装备了Logistic激活函数的神经元具有以下性质：
①其输出直接看作改良版分布，使得神经网络可以更好统计和学习模型进行结合；
②其可以看作一个软性门，用来控制其他神经网络输出信息的数量。


对比两个函数的形状，Tanh函数的输出是零中心化的，但是Logistic函数的输出恒大于0，非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移，进一步使得梯度下降的收敛速度变慢。

零中心化：函数输出值的均值为0（即对称于原点）。Tanh函数的输出范围是（-1，1）。均值为0；

4.1.1.1 Hard-Logistic函数和Hard-Tanh函数

Logistic函数和Tanh函数计算开销大。因为这两个函数在0附近 近似线性，两端饱和。所以，这两个函数可以通过分段函数来近似。

4.1.2 ReLU函数

ReLU（修正线性单元），是目前神经网络中经常使用的激活函数。实际上是一个斜坡函数。
定义为：

优点：
①计算高效：采用ReLU的神经元是需要进行加、乘、比较的操作；
②该函数具有生物学合理性，有单侧抑制，宽兴奋边界。
Sigmoid型激活哈桑农户会导致一个非稀疏的神经网络，但是ReLU却具有很好的稀疏性，大约50%的神经元会处于激活状态。
③ReLu函数是左饱和函数，当x > 0 时导数为1，在一定程度上缓解了神经网络的梯度消失问题，加速下降的收敛速度。
缺点：
①ReLU函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，影响下降的效率。
②ReLU神经元在训练时容易死亡。在训练时，若参数在一次不恰当的更新后，第一个隐藏层中的某个ReLu神经元在所有的训练数据上都不能被激活，会使得该神经元自身参数的梯度永远时0，在以后的训练中也永远不能被激活。这种现象是死亡ReLU问题，也可能发生在其他隐藏层。

4.1.2.1 带泄露的ReLU

带泄露的ReLU 在输入x < 0 时，保持一个很小的梯度。这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活。
传统的ReLU问题：当输入为负时，梯度为0，导致神经元可能永久死亡。LeakyReLU可以解决这个问题。

4.1.2.2 带参数的ReLU

带参数的ReLU引入一个可学习的参数。不同神经元可有不同参数。

其中α是x <= 0 时函数的斜率。因此，PReLU时非饱和函数，若α = 0，则PReLU会退化为ReLu。若α是一个很小的常数，则PReLU可以看作是带泄露的ReLU。

4.1.2.3 ELU函数

ELU（指数线性单元），是一个近似的零中心化的非线性函数。

4.1.2.4 Softplus函数

Softplus函数可以看作是ReLU的平滑版本。

Softplus函数其导数刚好是Logistic函数。没有稀疏激活性。
下面是ReLU、Leaky ReLU、ELU、Softplus 的形状对比

下面是ReLU、Leaky ReLU、ELU、Softplus 的梯度对比

4.1.3 Swish函数

Swish函数是一种自门控激活函数。

当σ(βx)接近于1时，门处于“开”状态，激活函数的输出近似于x本身。当σ(βx)接近于0时，门的状态为“关”，激活函数的输出近似于0；

当β = 0时，Swish函数变成线性函数。当β = 1时，Swish函数在x > 0时近似线性，在x < 0 时近似饱和，同时具有一定的非单调性。当β -> 正无穷时，σ(βx) 趋向于离散的0-1函数，Swish函数近似于ReLU函数。因此，Swish函数可以看作线性函数和ReLU函数之间的非线性插值函数，其程度由参数β控制。

4.1.4 GELU函数

GELU（高斯误差线性单元）是一种通过门控机制来调整其输出值的激活函数，和Swish函数类似。
其核心思想是将输入 x 与高斯分布的累积分布函数（CDF）结合。公式为：

特点：
①通过输入值 x 在高斯分布中的概率来“门控”输出，实现非线性变换。
②高斯分布的CDF是S型函数，因此GELU具有平滑的非线性特性。

由于高斯分布的累积分布函数为S型函数，所以，GELU函数可以用Tanh函数或Logistic函数近似。

3. 与Swish函数的关系

Swish函数定义为 Swish(x)=xσ(βx)，其中 β 是可学习参数。
当GELU用Sigmoid近似且系数 β=1.702 时，两者形式一致。因此，GELU是Swish的一种特殊情形。

4.与其他激活函数的对比

ReLU：GELU在负值区域非零，允许少量负值信息通过，避免“死神经元”。
Swish：GELU的理论基础更明确（基于高斯分布），而Swish更通用（参数可调）。

4.1.5 Maxout单元

Maxout 单元是一种分段线性激活函数
其核心特点是：

输入为向量：不同于传统激活函数（如 ReLU、Sigmoid）接收标量输入，Maxout 的输入是上一层神经元的全部原始输出向量
x=[x 1,x 2,…,x D]。
多组线性变换：通过 K 组独立的权重向量 w k 和偏置 b k，生成 K 个候选线性输出 z k。
取最大值输出：最终输出是这 K 个候选值中的最大值，即 maxout(x)=max(z 1 ,z 2,…,z K )。

4.2 网络结构

人工神经网络主要由大量得神经元以及它们之间得有向连接构成。因此考虑三方面：
①神经元得激活规则：
主要是指神经元输入到输出之间的映射关系，一般为非线性连接。
②网络的拓扑结构：
不同神经元之间的连接关系
③学习算法：
通过训练数据来学习神经网络的参数。
目前常用的网络结构有三种：

4.2.1 前馈网络

前馈网络中各个神经元按接受信息的先后分为不同的组。每一组都可以看成是一个神经层。每一层中的神经元接收前一层神经元的输出，并输出到下一层神经元。
整个网络中的信息是朝一个方向传播。并且前馈网络是无反馈连接：数据从输入层逐层传递到输出层，没有环路或反向传播路径（区别于循环神经网络RNN）。
2. 典型结构
①全连接前馈网络（Fully Connected Feedforward Network）：
每一层的神经元与下一层的所有神经元相连。
例如：多层感知机（MLP）。
②卷积神经网络（CNN）：
通过局部连接（卷积核）和权值共享减少参数，适合处理网格数据（如图像）。

4.2.2 记忆网络

1.核心定义
记忆网络（也称反馈网络）是一类具有记忆功能的神经网络，其特点是：

①动态状态：神经元可接收自身或其他神经元的历史信息，状态随时间变化。
②循环结构：信息传播可以是单向循环（如RNN）或双向交互（如玻尔兹曼机），结构上表现为有向循环图或无向图。
③外部记忆扩展：通过引入外部存储单元（如神经图灵机），显式增强网络的记忆容量。

2.典型模型

模型名称	特点
①循环神经网络（RNN）	通过隐藏状态传递历史信息，适合处理时序数据（如文本、语音）。
②Hopfield网络	能量模型，通过无向连接实现联想记忆，用于优化和模式恢复。
③玻尔兹曼机（BM）	概率生成模型，含隐藏层和可见层，通过随机采样学习分布。
④受限玻尔兹曼机（RBM）	概率生成模型，含隐藏层和可见层，通过随机采样学习分布。
⑤神经图灵机（NTM）	引入外部记忆矩阵和读写头，模拟计算机的存储机制。

4.2.3 图网络

1.核心定义
图网络是专门处理图结构数据的神经网络，其特点包括：
①输入形式：数据以图（Graph）形式表示，包含节点（Nodes）、边（Edges）和全局属性。
②泛化能力：是前馈网络和记忆网络的泛化，可处理非欧几里得数据（如社交网络、分子结构）。
③信息传递机制：节点通过聚合邻居信息更新自身状态（消息传递）。
2.典型模型

模型名称	核心机制
①图卷积网络（GCN）	通过邻接矩阵归一化聚合邻居信息
②图注意力网络（GAT）	引入注意力机制，动态学习邻居节点的重要性权重
③消息传递神经网络（MPNN）	通用框架，分“消息传递”和“状态更新”两步

神经网络是一种连接主义模型，也就是PDP(Parallel Distributed Processing)模型（PDP（并行分布式处理）模型是连接主义道德一种实现形式）。
它具有以下关键特征：

1. 信息表示的分布式特性
   分布式存储：信息不是局部存储在单个单元中，而是分散在整个网络的连接权重模式中

叠加存储：同一组神经元可以同时存储多个记忆或模式

内容寻址：可以通过部分信息恢复完整模式(联想记忆)

2. 并行处理机制
   大规模并行性：所有处理单元同时进行计算

集体计算：结果由大量简单单元的协同活动决定

非线性交互：单元间通过非线性函数相互作用

3. 连接权重的重要性
   知识存储在连接中：系统的"知识"体现在单元间的连接权重上

可塑性：连接权重可通过学习调整(如Hebbian学习规则)

适应性：系统能通过调整权重适应新任务

4. 处理单元的特性
   简单处理单元：每个单元只执行简单计算(如加权求和+激活函数)

非符号性：单元活动不直接对应符号或概念

数值性：信息表示为连续的激活值而非离散符号
与符号主义的对比

特性	PDP/连接主义模型	符号主义模型
信息表示	分布式(连接权重模式)	局部(离散符号)
处理方式	并行	串行
知识存储	隐式(难以解释)	显式(可解释)
学习方式	参数自动调整	规则手工编码
容错性	强	弱

4.3 前馈神经网络（全连接神经网络，多层感知器）

• 各神经元分别属于不同层，层内无连接
• 相邻两层间的神经元全部两两连接
• 整个网络中无反馈，信号从输入层向输出层单向传播，可用有向无环图表示。
  
  
  注意： ①神经网络的层数一般不包括输入层，只计算隐藏层和输出层。
  ②神经网络的层数、第l层神经元的个数、第l层神经元的激活函数这些都是超参数。
  
  注意： ①第一个公式地本质是仿射变换。
  对于向量空间中的点 x ∈ ℝⁿ，仿射变换可表示为：T(x) = Wx + b

仿射变换 是线性变换的扩展，由线性变换和平移变换组合而成

前馈计算：

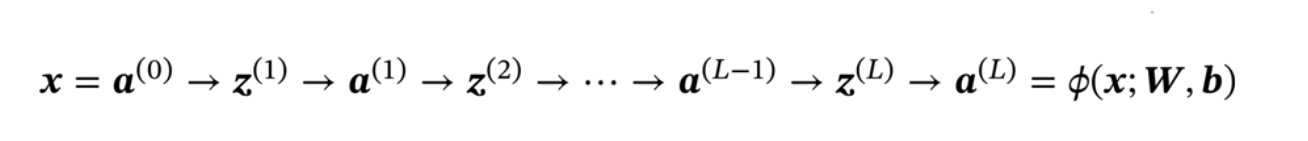
4.3.1 通用近似定理

（理论不做过多解释）
结论：
**通用近似定理说明了：**神经网络的计算能力可以去近似一个给定的连续函数

4.3.2 应用到机器学习

4.3.4 参数学习

1.交叉熵损失函数：ℒ(y, ŷ) = -yᵀlog(ŷ)

• y：one-hot编码的真实标签（如[0,1,0]表示第二类）
• ŷ：模型预测的概率分布（如[0.1,0.7,0.2]）
• 物理意义：当预测概率ŷ与真实标签y差距越大，损失值越高

2.结构化风险函数：ℛ(W,b) = (1/N)∑ℒ(y⁽ⁿ⁾,ŷ⁽ⁿ⁾) + (1/2)λ‖W‖²_F（学习准则）

• 第一项：所有样本的平均交叉熵损失
• 第二项：L2正则化（权重衰减），控制模型复杂度
• λ：调节正则化强度的超参数（λ越大惩罚越重）
  
  3.网络参数通过梯度下降法进行学习，每次迭代中，第 l 层 的参数更新方式：
  

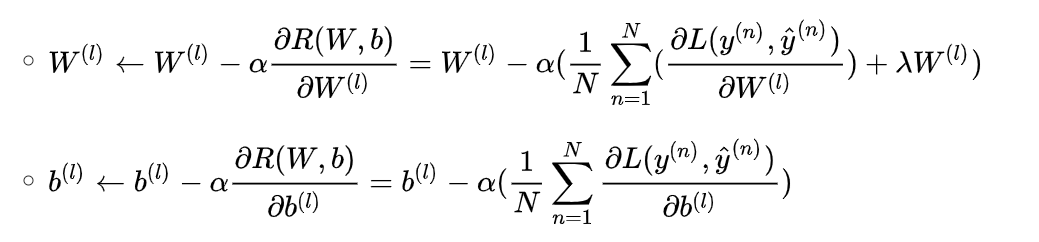
α是学习率。使用反向传播算法来高效地计算梯度。
一种更通用的计算梯度算法是：自动微分

4.4 反向传播算法

分母布局是列向量，分子布局是行向量。

用随机梯度下降法进行参数学习，需要计算损失函数关于每个参数的梯度

上面的公式将利用链式法则进行展开。
链式法则：

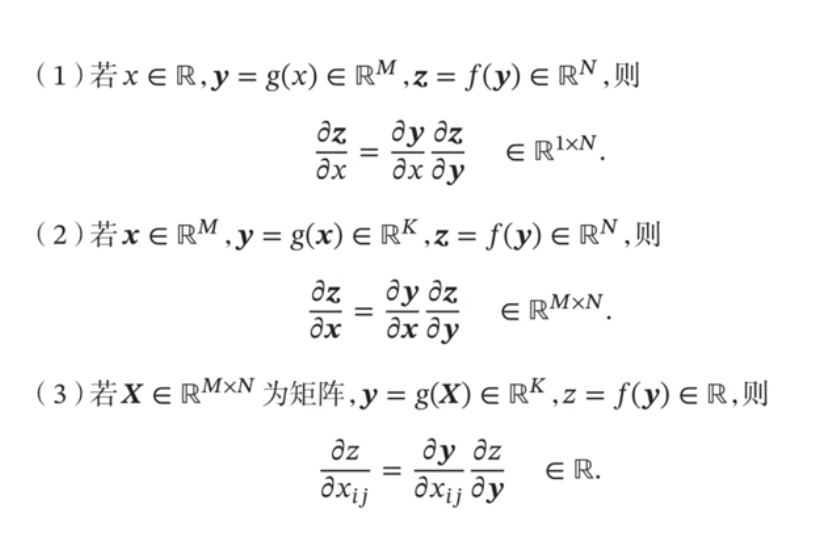
• 情况1：向量对标量的链式求导
• 情况2：向量对向量的链式求导
• 情况3：标量对矩阵的求导
  根据上面偏导数的公式，得到求3个偏导数式子即可。
  
  在这个式子中，z是列向量，w(ij)是标量，所以求导结果是一个行向量。只有z(i)对w(ij)的求导不为0，是因为
  第二个偏导数：（反向传播）
  
  
  
  
  **fl(.)**是按位函数
  

第三个偏导数：

使用误差反向传播算法的前馈神经网络训练过程有以下步骤：
①前馈计算每一层的净输入和激活值，直到最后一层；
②反向传播计算每一层的误差项。（就是求第2个偏导数）；
③最后计算每一层参数的偏导数，并更新参数（就是求第1个和第3个偏导数，之后再按照4.3.3 参数学习里面的第3部分进行参数更新）。

按照上面的式子，代入到损失函数关于每个参数的梯度的式子中，得到：

4.5 计算图和自动微分

（其实还有数值微分和符号微分，这里不再写，大家可以自行了解）
1.自动微分是一种可以对一个（程序）函数进行计算导数的方法

• 处理的对象是一个函数或一段程序
• 是目前大多数深度学习框架的首选
• 基本原理：所有的数值计算可以分解为一些基本操作，包括 + 、-、*、/ 和一些初等函数 exp、log、sin、cos等，并构成一个计算图，然后用链式法则来自动计算一个复合函数的梯度
• 无需事先编译，在程序运行阶段边计算边记录计算图，计算图上的局部梯度都直接代入数值进行计算，然后用前向模式或反向模式计算最终的梯度。
  

2.自动微分分为：

• 前向模式：按计算图中计算方向的相同方向来递归地计算梯度
• 反向模式：按计算图中计算方向的相反方向来递归地计算梯度
• 反向模式和反向传播的计算梯度的方式相同。

3.为什么神经网络选择反向模式？
- 输出为标量：损失函数 R 的输出维度 M = 1，反向模式仅需 1次计算。
- 参数规模大：输入维度 N（参数量）极大，前向模式需要 N 次计算，效率极低。
- 链式法则优化：反向传播利用动态规划思想，避免重复计算中间变量的梯度。
（上面的两张图就是解释这个问题的）
如果函数和参数之间有多条路径，可以将这多条路径上的导数再进行相加，得到最终的梯度。
4.反向传播算法（自动微分的反向模式）
前馈神经网络的训练过程可以分为以下3步：
①前向计算每一层的状态和激活值，直到最后一层；
②反向计算每一层的参数和偏导数；
③更新参数。（其实跟4.4 反向传播算法里面介绍的是一样的，只不过是用这里提到的前向计算和反向计算再表述一遍）
5.计算图按构建方式可分为：
①静态计算图：在编译时构建计算图，构建好后在程序运行时不能改变
特性：构建时可以进行优化，并行能力强，但灵活性比较差
实例：Tensorflow
②动态计算图：在程序运行时动态构建
特性：不容易优化，难以并行计算，但灵活性比较高
实例：Pytorch、Tensorflow 2.0

6.Keras使用展示
展示如何使用Keras（一个高级神经网络API）在30秒内快速构建并训练一个简单的全连接神经网络。

from keras.models import Sequential  
from keras.layers import Dense, Activation  
from keras.optimizers import SGD
#1.导入必要的模块.Sequential: 线性堆叠模型，用于构建层与层之间简单连接的神经网络；Dense: 全连接层；Activation: 激活函数层；SGD: 随机梯度下降优化器
model = Sequential()
#2.创建一个空的顺序模型，后续可以逐层添加网络结构
model.add(Dense(output_dim=64, input_dim=100))  
model.add(Activation("relu"))  
model.add(Dense(output_dim=40))  
model.add(Activation("softmax"))
#3.构建了一个两层的全连接神经网络：
#第一层:输入维度: 100 (input_dim=100)；输出维度: 64 (output_dim=64)；使用ReLU激活函数
#第二层:输出维度: 40 (自动继承上一层的64作为输入)；使用Softmax激活函数（适用于多分类问题）
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
#4.编译模型
#配置模型的学习过程：loss: 使用分类交叉熵损失函数（适用于多分类问题）；optimizer: 使用随机梯度下降(SGD)优化器 ；metrics: 在训练过程中监控准确率(accuracy)
model.fit(X_train, Y_train, nb_epoch=5, batch_size=32)
#5.训练模型
#X_train: 训练数据特征 ；Y_train: 训练数据标签 ；nb_epoch=5: 训练5个完整周期（整个数据集迭代5次）；batch_size=32: 每次梯度更新使用32个样本
loss = model.evaluate(X_test, Y_test, batch_size=32)
#6.评估模型

4.6 优化问题

神经网络的参数学习比线性模型要更加困难，主要原因有两点：
①非凸优化问题
②梯度消失问题

4.6.1 非凸优化问题

神经网络的优化问题是一个非凸优化问题
以下面最简单的两层

（可视化这里的代码优点问题，跑出来的图不太对…）

上述可视化结果分析

1. 平方误差损失曲面特征：
   ①存在多个局部极小点
   ②损失曲面较为"平缓"
   ③梯度变化相对均匀

2. 交叉熵损失曲面特征：
   ①同样存在多个局部极小点
   ②在y接近0的区域梯度变化剧烈
   ③整体形状更为"陡峭"

4.6.2 梯度消失问题/梯度弥散问题

**减轻梯度消失问题的方法：**使用导数比较大的激活函数，eg. ReLU

4.7 总结