【数据结构】·励志大厂版(复习+刷题):二叉树


前引:哈喽小伙伴们!经过几个月的间隔,还是逃脱不了再次复习的命运!!!本篇文章没有冗杂的闲话,全是干货教学,带你横扫二叉树的几种遍历,怎么前序、、中序、后续?如何识别?二叉树其实难得就是它的递归,代码量其实并不多,插入与遍历打印都是递归,但是本篇文章完全就是buuff加身,看完还不会二叉树的欢迎在评论区留言,小编接受检讨!~~正文开始
目录
知识点速览
树的名词解释
二叉树的四种遍历
二叉树性质:
满二叉树:
完全二叉树:
练习题(1)
练习题(2)
练习题(3)
练习总结
二叉树实现
定义结构体
初始化
新增节点
前序遍历
中序遍历
后序遍历
二叉树OJ(1)
二叉树OJ(2)
二叉树OJ(3)
二叉树OJ(4)
知识点速览
在学二叉树之前我们需要作为补充了解树的几个名词概念
树的名词解释

节点的度:一个节点含有子节点的个数。例如A的度:为6
叶节点或终端节点:度为0的节点。例如:B、C、H、P、Q、N都为叶节点
分支节点或非终端节点:度不为0的节点。例如:D、A、G、J都为分支节点
双亲节点或父节点:若一个节点有度(即有子节点),该节点为父节点。例如:A、D、E为父节点
孩子节点或子节点:也就是拥有度的这些节点的下一层节点。例如:B、C、D都为子节点
兄弟节点:拥有相同父节点的子节点。例如:I、J是兄弟节点,K、L、M是兄弟节点
树的度:孩子节点最多的度。例如:这棵树中孩子节点最多的是A节点,那么这颗树的度为6
节点的层次:从根节点开始从1开始算。例如:J的层次为3,Q的层次为4
树的高度或者深度:树中节点的最大层次。例如:这棵树节点层次最大的是P与Q,树最大层次为4
节点的祖先:从根节点到该分支的所有节点。例如:A是所有节点的祖先。G不是L的祖先
子孙:以某节点为根的子树中的任意节点。例如:所有节点是A的子孙。Q不是D的子孙
森林:由 m (m>0)棵互不相交的多棵树的集合称为森林
二叉树的四种遍历

这四种遍历其实并不难,下面小编带大家深刻理解这四种遍历!
首先前、中、后三种遍历中的的这三个关键字“前”“中”“后”都是根据根节点而言的,左子树永远在右子树前面,(大家注意观察根节点与遍历方式的位置!)它的遍历都是将一个子树对应位置遍历完之后再遍历又一个子树,理解:每次不断分成不同大小的树,然后递归到末尾,再原路返回。小编以中序遍历为列,仔细讲解一下!最好的理解方式就是动手画到不出错为止!
前序遍历:根节点、左子树、右子树
遍历顺序:A->B->D->NULL->NULL->E->NULL->NULL->C->NULL->F->NULL->NILL
中序遍历:左子树、根节点、右子树
以A为根节点,先访问左子树,也就是这部分
再以B为根节点,再访问左子树,也就是这部分 
再以D为根节点,访问其左子树,已经是这部分
此时已经到底了无法再分,访问“NULL”,然后访问根节点“D”,再访问D的右子树 “NULL”
以此类推,直到不能分为止,这里是利用了递归到NULL就返回的原理。
遍历顺序:NULL->D->NULL->B->NULL->E->NULL->A->NULL->C->NULL->F->NULL
后序遍历:左子树、右子树、根节点
遍历顺序:NULL->NULL->D->NULL->NULL->E->B->NULL->NULL->NULL->F->C->A
层序遍历:一层一层访问
遍历顺序:A->B->C->D->E->NULL->F->NULL->NULL->NULL->NULL->NULL->NULL
二叉树性质:
满二叉树:
概念:每个父节点除最后一层的叶子节点外都有两个子节(满二叉树是一种特殊的完全二叉树)

性质(1): 假设根节点层数为0,树层数为K,那么它的节点个数N为 2^K-1,高度为 logN
推论:第一层有1个节点(2^0),第二层有2个节点(2^1),第三层有4个节点(2^2),以此类 推,得到节点数 N = 2^0 + 2^1 + 2^2 + 2^3 + ...... = 2^K -1 . 此时 K = log(N+1)
性质(2):假设根节点层数为0,二叉树第 K 层的节点数最多为 2^K 个
性质(3):任意一棵二叉树,假设度为 0 的节点数为 n0 ,度为 2 的节点数为 n2 ,满足以下关系
满足 n0 = n2+1(只记结论)
例如:假设现在有这样一棵树,度为0的节点数有5个,度为2的节点数有4个,满足 5=4+1

完全二叉树:
概念:只有最后一层不满,且最后一层从左到右是连续的

性质:节点总数 N 满足 N < 2^K-1 ,高度 K =log(N+1)
推论:我们无法确定完全二叉树具体的节点个数,只能通过满二叉树进行推理![]() ,其它树亦如此
,其它树亦如此
练习题(1)

套用公式:度为0的节点数(叶子节点)= 度为2的节点数 + 1 ,得到最终答案 200
练习题(2)


这是一棵完全二叉树,它的节点组成是度为0的、度为1的、度为2的总和,也就是:
x0 + x1 + x2 =2n ,同时套用公式 x0 = x2 + 1,两个结合得到:2 * x0 + x1 - 1 = 2n
我们观察图,发现完全二叉树度为1的节点只有一个,因此 x1 = 1,那么算出来得到 x0 = n
练习题(3)

我们假设高度为 h ,最后一层缺了 x 个,同时知道满二叉树是特殊的完全二叉树
那么满足: 2^h-1 - x = 531. 同时 x 的范围应该在 【0,2 ^ h-1】,x 的范围如下图所示:
直接一个都不缺,为0个
最多缺一个,x为2 ^ h-1个 
结合这两个关系式,去套,最后得出只有当高度为10时满足 (注意这里的层数从0开始)
练习总结
除了直接套用公式的题,如果出现节点总数求某个变量的值,似乎都要去通过建立方程表示节点总数,表示方式一般有两种:(1)不同度的节点数之和(2)通过节点总数满二叉树计算公式去计算
二叉树实现
定义结构体
咱们按照二叉树的结构,定义一个左子节点、右子节点、一个数据域就行了,这是最简单的定义
//重定义类型
typedef int Datatype;typedef struct Tree
{//左孩子节点struct Tree* left;//右孩子节点struct Tree* right;//数据域Datatype data;
}Tree;初始化
初始化我们开辟一个根节点返回就行了,以后将其作为参数再去连接左右节点
//初始化树
Tree* Perliminary(Datatype data)
{//开辟根节点Tree* newnode = (Tree*)malloc(sizeof(Tree));//判断有效性if (newnode == NULL){printf("节点开辟失败\n");return NULL;}//初始化指针newnode->data = data;newnode->left = NULL;newnode->right = NULL;return newnode;
}新增节点
首先我们初始化了一个根节点,新增的节点值与根节点的值进行比较
如果小于根节点的值,递归左子树;如果大于根节点的值,递归右子树;
随着递归的不断调用,它的根节点会不断改变,如果为空,就返回新增的节点
最后回到最初的根节点
//新增节点
Tree* Capacity(Tree* TreeNode, Datatype data)
{//如果是空节点就插入if (TreeNode == NULL){return Perliminary(data);}//如果是非空节点就继续递归//较小就插入到左子节点if (data < TreeNode->data){TreeNode->left = Capacity(TreeNode->left, data);}elseTreeNode->right = Capacity(TreeNode->right, data);//回到原初的根节点return TreeNode;
}前序遍历
首先递归到子树的极端,遇到空就开始返回,再调整打印顺序

//前序遍历
Tree* Preorder(Tree* TreeNode)
{if (TreeNode == NULL){return;}//根节点printf("%d ", TreeNode->data);//左子树Preorder(TreeNode->left);//右子树Preorder(TreeNode->right);
}中序遍历

//中序遍历
Tree* Mid(Tree* TreeNode)
{//如果遇到空返回if (TreeNode == NULL){return;}//左子树Mid(TreeNode->left);//根节点printf("%d ", TreeNode->data);//右子树Mid(TreeNode->right);
}后序遍历

//后序遍历
Tree* Behind(Tree* TreeNode)
{//递归到深处,如果是空就开始返回if (TreeNode == NULL){return;}//左子树Behind(TreeNode->left);//右子树Behind(TreeNode->right);//根printf("%d ", TreeNode->data);
}二叉树OJ(1)

假设现在有这样一棵树
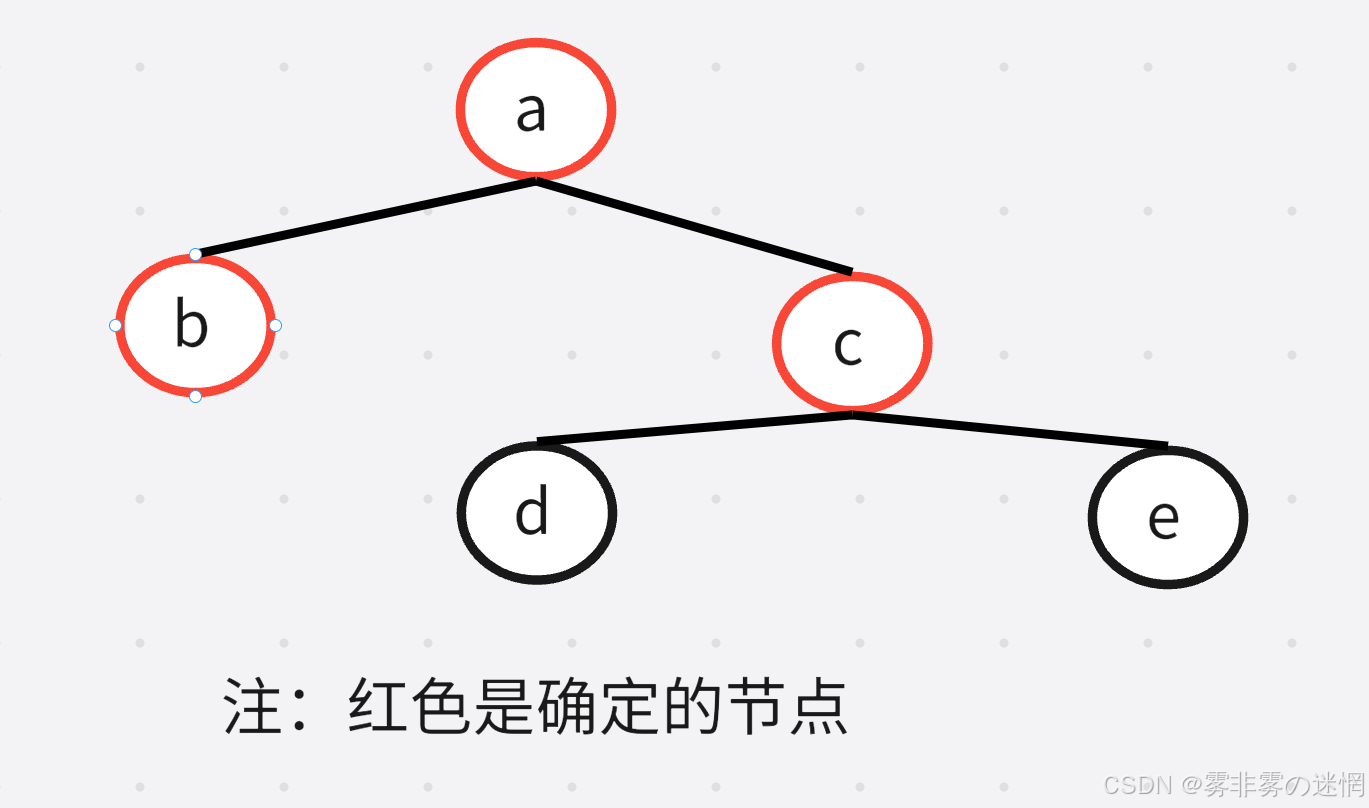
它的中序遍历结果为:D->B->E->A->F->C 后序遍历结果为:D->E->B->F->C->A
按照中序顺序,我们去推得到 b 应该在最左边;按照后序顺序,我们得到 a 应该是根节点
所以 a 是在根节点,再根据中序顺序,得到 a 的左边是 b ,同时 c 是 a 的右子树,这样就能推出
二叉树OJ(2)


题目链接:https://leetcode.cn/problems/binary-tree-preorder-traversal
题目是要我们将前序遍历的节点结果返回
思维讲解:
流程:用一个空间将每次遍历的值存储起来,然后返回
(1)首先我们开辟数组,数组的空间大小最好是由节点个数决定,因此先遍历二叉树计算节点
return root==NULL? 0 : treesize(root->left) + treesize(root->right) + 1;
(2)然后开辟对应大小的数组空间
//计算节点个数int size=treesize(root);//开辟空间int* arr=(int*)malloc(sizeof(int)*size);(3)接下来就是递归遍历储存节点,但是要考虑一个问题,如果在这个函数里面去递归,那么每次调用都要去开辟空间,所以我们选择再开一个来进行递归遍历,参数是根节点、空间指针、计数
注意:计数的 i 应该取地址,因为递归会开辟多个函数,不然每次 i 都只是一次拷贝而已
//存进空间int i=0;preorder_Traversal(root,arr,&i);(4)然后将之前的前序遍历的打印换成储存即可
//前序遍历if(root==NULL){return;}arr[*i]=root->val;++(*i);preorder_Traversal(root->left,arr,i);preorder_Traversal(root->right,arr,i);(5)最后:这是整型指针空间,返回的只是一个元素,所以按照题目要求,还有设置元素个数
*returnSize = size;return arr;二叉树OJ(3)

题目链接:https://leetcode.cn/problems/binary-tree-postorder-traversal
此题和上面这题几乎一模一样,就作为思维训练巩固给大家了!记得独立完成哦!

二叉树OJ(4)

题目链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree

思维讲解:此题是求二叉树的最大深度,二叉树最大深度就是最大层数

(1)假设有一棵树如上图,它的深度是3。这里采用分治思想,先求左子树的深度为3,再求右子 树的深度为2,再对比找最大值,然后返回 最大值+1(因为一个节点层次为1)
(2)下面我们来实现,先递归左子树,再递归右子树,那么它是如何计算子树深度的呢?
假设递归到左子树的末尾,q 的左子树右子树都为空,返回0,此时0>0为假,返回0+1
那么q拿到的就是1

假设递归到 c ,c的左右子树都不为空,继续递归,此时d的左右子树都为空返回,0>0为假d拿到1
同理,e拿到1;1>1为假,c拿到的就是1+1。其它节点类推即可

小编期待与你的下次相遇 !

