数组滑动窗口单调栈单调队列trick集【leetcode hot100 c++速查！！！】

我们尝试将这三类问题放在一个专题中进行讨论，是因为它们有很多公共的部分。

• 它们其实都是在处理窗口内的问题
• 讲到窗口，就难免涉及到窗口的伸缩问题，常见的伸缩方式有：
  • 窗口两端往同一个方向移动(但移动速度可能不同，窗口大小也是动态变化的)。
  • 窗口两端往两个相反方向扩展(体现为窗口总是在变大)。
  • 窗口中只有一端在扩展
• 滑动窗口相关的问题，一般是考虑窗口内的所有元素
• 单调栈&队列，一般是考虑窗口内的子序列，这个子序列具有单调性(递增/递减)
• 单调栈&队列，其实恰好对应窗口的伸缩方向

栈

经典模版题-括号

20. 有效的括号 - 力扣（LeetCode）

class Solution {
public:stack<char> stk;//使用hash表unordered_map<char,char> hash={{'(', ')'},{'[', ']'}, {'{', '}'}};bool isValid(string s) {for(auto c:s){if(!stk.empty()&&hash[stk.top()]==c) stk.pop();else stk.push(c);}return stk.empty();}
};

最小栈

155. 最小栈 - 力扣（LeetCode）

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

class MinStack {
public:stack<int> a,b;MinStack() {  }void push(int val) {a.push(val);//b始终是栈a中的最小元素if(b.empty()) b.push(val);else b.push(min(b.top(),val));}void pop() {a.pop();b.pop();}int top() {return a.top();}int getMin() {return b.top();}
};

字符串解码

394. 字符串解码 - 力扣（LeetCode）

以下用a2[b]举例子：

1. 当遇到’[‘，把’[‘和与之匹配的’]‘之间的字母需要重复的次数和’['之前的字符进栈，本例中进栈{2,a}
2. 当遇到’]'，代码中的字符串res即：b,就是要重复的字母，此时出栈之前进栈的{2,a}，res变成a+2*b = abb

class Solution {
public:string decodeString(string s) {//单栈实现vector<pair<int,string>> st;string res="";int repeat=0;for(char c:s){//两位及以上需要连乘if(isdigit(c)) repeat=repeat*10+c-'0';else if(c=='['){//入栈st.push_back({repeat,res});repeat=0,res="";//重新计算}else if(c==']'){//取栈顶元素auto [reSub,strSub]=st.back();//弹出栈顶元素st.pop_back();//重复添加res多次到subStr中while(reSub--) strSub+=res;res=strSub;}//字母则保存在res中else res+=c;}return res;}
};

每日温度

739. 每日温度 - 力扣（LeetCode）

即找右侧第一个比自己大的数：维护后缀窗口递增

class Solution {
public:vector<int> dailyTemperatures(vector<int>& temperatures) {int n=temperatures.size();stack<int> stk;//记录下标值vector<int> res(n,0);//维护后缀窗口递增序列for(int i=n-1;i>=0;i--){//弹出单调栈中比自己小的元素while(!stk.empty()&&temperatures[i]>=temperatures[stk.top()]) stk.pop();if(!stk.empty()) res[i]=stk.top()-i;//当前元素入栈stk.push(i) ;}return res;}
};

柱状图的最大矩形

84. 柱状图中最大的矩形 - 力扣（LeetCode）

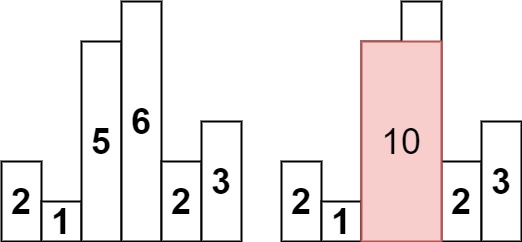
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();//用于保存最大宽度vector<int> w(n,1);stack<int> stk;//左侧可扩展的最大宽度for(int i=0;i<n;i++){//维护前缀窗口递减[右向左]while(!stk.empty()&&heights[stk.top()]>=heights[i]) stk.pop();if(stk.empty()) w[i]+=i;//左边没有比其矮的柱子,从i=0开始扩展//不包括stk.top()这个元素else w[i]+=i-stk.top()-1;stk.push(i);}int res=0;//栈清空while(!stk.empty()) stk.pop();//右侧可扩展的最大宽度for(int i=n-1;i>=0;i--){//维护后缀窗口递减while(!stk.empty()&&heights[stk.top()]>=heights[i]) stk.pop();if(stk.empty()) w[i]+=n-i-1;else w[i]+=stk.top()-i-1;stk.push(i);res=max(res,heights[i]*w[i]);}return res;}
};

堆

数组中的第k个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

小根堆维护堆顶为k个元素的最小值，每个元素进行判断，更大的进堆，最终队顶为k个最大数的最小值。

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {//定义元素类型 容器类型 比较器(默认大根堆less<int>)priority_queue<int ,vector<int>, greater<int>> pq;for(int curr:nums){//小根堆维护堆顶为k个元素的最小值if(pq.size()<k) pq.push(curr);else{//如果curr比根堆元素大 则有可能是第k大元素 否则不可能if(pq.top()<curr) {pq.pop();pq.push(curr);}}}return pq.top();}
};

前k个高频元素

347. 前 K 个高频元素 - 力扣（LeetCode）

计算频率作为数组元素再进行排序

class Solution {
public:vector<int> topKFrequent(vector<int>& nums, int k) {unordered_map<int,int> freq;//map存放各元素出现频率for(int x:nums) freq[x]+=1;priority_queue<pair<int,int>> pq;for(auto& p :freq)//将频率放在前面方便排序pq.push({p.second,p.first});//此时pq为根据频率排序的大根堆vector<int> res(k);//取大根堆的前k个元素即可for(int i=0;i<k;i++) {res[i]=pq.top().second;pq.pop();}return res;}
};

数据流中的中位数

295. 数据流的中位数 - 力扣（LeetCode）

• MedianFinder() 初始化 MedianFinder 对象。
• void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
• double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。

class MedianFinder {
public://小根堆保存较大的一半 N/2或N+1/2priority_queue<int,vector<int>,greater<int>> sq;priority_queue<int,vector<int>,less<int>> bq;MedianFinder() { }void addNum(int num) {//奇数 需要向bq中添加一个元素if(sq.size()!=bq.size()){//不能确定sum是否应该在bq中 需先加入sq 找到sq的最小元素sq.push(num);//将sq的top最小元素插入bqbq.push(sq.top());sq.pop();}else {//偶数 需要向sq中添加一个元素bq.push(num);sq.push(bq.top());bq.pop();}}double findMedian() {//奇数返回sq.top() 偶数返回两个top的均值return sq.size()!=bq.size()?sq.top():(sq.top()+bq.top())/2.0;}
};

数组

最大子数组和

53. 最大子数组和 - 力扣（LeetCode）

某个数使得前缀和为负数则起始点在该位置之后！

class Solution {
public:int maxSubArray(vector<int>& nums) {long long sum=0;int n=nums.size();long long res=-1e5;for(int i=0;i<n;i++){//维护前缀和sum+=nums[i];res=max(res,sum);//如果遍历到当前位使得sum由正变负 则改变起始位置在该位之后if(sum<=0) sum=0;}return res;}
};

合并区间

56. 合并区间 - 力扣（LeetCode）

请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

按左端点进行排序，之后不断比对下一个左端点是否和上一个右端点有重叠。

class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {//按左边界进行从小到大排序sort(intervals.begin(),intervals.end());vector<vector<int>> res;//记录当前左右端点int l=intervals[0][0],r=intervals[0][1];//从第二个区间开始遍历for(int i=1;i<intervals.size();i++){//如果该区间左端点比r大 则前一区间需合并 重新开启l和rif(intervals[i][0]>r){res.push_back({l,r});l=intervals[i][0];r=intervals[i][1];}//扩充右端点relse  r=max(r,intervals[i][1]);}//只有满足条件才会push结果 最后一个区间也需要pushres.push_back({l,r});return res;}
};

轮转数组

189. 轮转数组 - 力扣（LeetCode）

• 翻转整个数组
• [0,k-1]翻转
• [k,n-1]翻转

class Solution {
public:void rotate(vector<int>& nums, int k) {k%=nums.size();//先翻转整个数组reverse(nums,0,nums.size()-1);//[0,k-1]翻转reverse(nums,0,k-1);//[k,n-1]翻转reverse(nums,k,nums.size()-1);}void reverse(vector<int>& nums,int st,int ed){while(st<ed){swap(nums[st],nums[ed]);st+=1;ed-=1;}}
};

除自身以外数组的乘积

238. 除自身以外数组的乘积 - 力扣（LeetCode）

请 **不要使用除法，**且在 O(n) 时间复杂度内完成此题。

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n=nums.size();vector<int> res(n,1);int pre=1;for(int i=0;i<n;i++){res[i]*=pre;//当前元素左边所有元素的乘积pre*=nums[i];}pre=1;for(int i=n-1;i>=0;i--){res[i]*=pre;//存储的是当前元素右边的所有元素的乘积//*=也保存了原来左边的乘积pre*=nums[i];}return res;}
};