基于C++实现人工智能—五子棋的目标识别

人工智能大作业报告

一、监督学习

1.1 问题描述

能够用拍照方式识别五子棋下棋过程中当前落子的位置，识别程序中应使用到监督学习算法。

1.2 方法描述

使用 yolov5 实现对五子棋的目标识别，使用编写的五子棋界面生成训练和测试数据。下载预训练模型后，进行迁移学习，训练得到识别黑白棋的模型。

1.3 步骤描述

利用五子棋界面生成训练数据

• 对于五子棋界面的实现，考虑到界面不是本次作业实现的主要目标，所以使用 tkinter 库来实现五子棋简易界面。
• yolov5 所用的标签格式为 [物体类型物体中心 x 值物体中心 y 值物体长度物体宽度]。随机生成五子棋局面，绘制界面，生成标签，训练数据大小为 200 张图片
• 生成训练数据的代码位于 Python/window/create_train_data.py 文件中。

下载 yolov5 项目，下载预训练模型

• yolov5 所用的模型代码来自 github 上的一个。考虑到黑白棋的特征明显，识别出来的难度不大，所以我使用的预训练模型为 YOLOv5s 模型。在进行 100 次的训练后能够较好地得到结果。

对模型进行训练

模型训练过程中准确率和召回率和 IoU 阈值为 0.5 时的 mAP 值变化如下：

准确率

召回率

mAP:0.5

图 1: 模型指标变化

可以看出模型效果随着训练逐渐变好。

1.4 结果分析

输入的测试图片和识别图片如下：

测试图片

识别图片

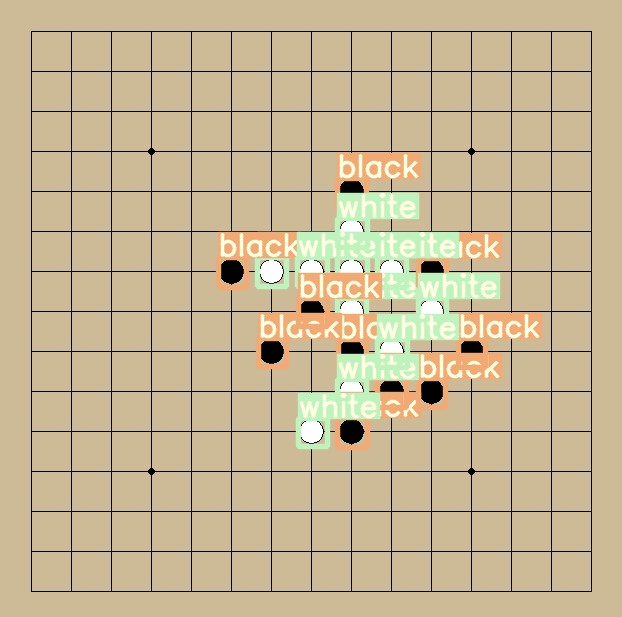
图 2: 模型预测图片可以看到白棋和黑棋被识别了出来。

二、博弈搜索

2.1 问题描述

采用一种博弈搜索算法，实现五子棋博弈程序，其中对棋局状态的判断采用人为设定函数方式。

2.2 方法描述

通过自定义的评估函数返回棋局评分，使用 alpha-beta 搜索，结合一定的优化方法，计算得到 ai 下一步所走的位置。

2.3 原理描述

AB 剪枝就是 minmax 搜索的优化。在 MAX 层，假设当前层已经搜索到一个最大值 X，如果发现下一个节点的下一层（也就是 MIN 层）会产生一个比 X 还小的值，那么就直接剪掉此节点。在 MIN 层，假设当前层已经搜索到一个最小值 Y，如果发现下一个节点的下一层（也就是 MAX 层）会产生一个比 Y 还大的值，那么就直接剪掉此节点。

当搜索到达了最大层数，对节点进行评分，根据不同节点评分进行剪枝。搜索完毕后，走分数最大的位置。

2.4 步骤描述

1.编写自定义的评估函数

评估函数采用了常用的根据形成的棋型打分的方式对于形成的不同棋型，如活四、活三、死四等，给予不同的分数。对于敌我双方分数的判定，没有进行特殊的分析方式，而是分别计算双方的总分，然后敌方分数降低一半进行相减，得到局面分数。

评估函数的实现方式在 C++/code_file/Evaluation.cpp 文件中。

2.编写获取搜索位置的函数

根据五子棋“战场”的局部性，我认为下载偏远地方的棋子对于胜率影响不大，所以对于一个位置，只有它周围有棋子的时候，才进行搜索。

可以根据启发式函数获取搜索位置，但我试着实现计算空位得分方式进行启发式搜索，发现结果反而更慢。。。于是就放弃了启发式搜索。

搜索位置函数实现方式在 C++/code_file/Get_position.cpp 文件中。

3.编写搜索函数

首先调用获取搜索位置函数获得搜索位置，然后进行 alpha-beta 搜索，当搜索到达最大层数时，调用评估函数，返回评估值。

在搜索的过程中，需要判断局面是否结束，如果敌方胜利，则上一步的落子是失败的，不能下在这。

搜索函数实现方式 C++/code_file/AB_search.cpp 文件中。

2.5 结果分析

设置搜索层数为 4 时，ai 搜索一些步骤耗费时间较长，可能是评估函数定义得不够好，导致 alphabeta 发生的剪枝次数较少，ai 搜索轻情况太多，搜索时间较长。

设置搜索层数为 2 时，ai 能够较快地得出结果，并且具有一定的棋力。

对于搜索效果的进一步优化，我认为从增加剪枝方法，启发式方法进行优化，搜索过程中存在搜索重复局面的情况，所以可以通过一种算法保存局面和评分，如果在次搜索到同一局面，可以直接获得分数，不用继续搜索。启发式方法可能的做法为检测双活三和冲四等等，缩小搜索范围。

三、进化计算

3.1 问题描述

将上述博弈搜索算法中判断棋局状态的函数改为一种人工神经网络模型，并采用进化计算方法对该人工神经网络模型来进行学习，使得五子棋博弈程序的下棋水平不断提高。

3.2 方法描述

在进行方法说明前，我得吐槽一句，从一开始我就对遗传算法优化神经网络的效果是不报任何希望的。不说 neat 算法同时进化网络结构和权值，所耗的时间无法估计。找了一个利用遗传算法优化网络权值的论文，一看，方法是首先优化得到粗略的权值，最后还是用梯度下降训练权值，好家伙，再一看，才几百个参数。对于 225 的输入数量，上万的权值数，这点参数还不够塞牙缝的。

我将这个问题视为一个多分类问题，输入当前局面，输出为各点的落子概率。以网上找的棋局作为训练数据，进行监督学习。

首先确定网络结构，输入层节点数为 225，一个隐含层，节点数为 300，输出层，节点数为 225，最后输出值进行 softmax 归一化，预测下一步的落子。适应度函数为交叉熵的倒数，标签为棋手下一步的落子位置。根据各网络的适应度进行选择操作，之后进行交叉，变异操作，不断进行迭代。

3.3 原理描述

开始时本来不准备用监督学习的，打算以第二位的搜索 ai 作为环境，坚持的时间越久，适应度越高。但是每个网络都在 12 步之内就输掉，适应度也一直不会升高。想想还是不太靠谱，就换成监督学习了。

多分类的监督学习任务常用的损失函数为交叉熵函数，用遗传算法训练网络权值，让交叉熵函数最小，所以以交叉熵函数的倒数作为适应度函数。

3.4 步骤描述

实现代码位于/Python/Evaluation/Net.py 文件中。

1.适应度函数

输入棋局中某一时刻的棋面，通过网络得到下到每个点的概率，以棋手下一步的落子位置作为标签，计算交叉熵，因为要求交叉熵越小越好，所以适应度为交叉熵的倒数。

2.选择操作

计算 10 个网络的适应度，根据轮盘赌选择保留的种群。

3.交叉操作

对于每一个种群，生成一个随机数，如果小于 0.88，则加入队列进行交叉操作。

对于一次交叉操作，随机生成两个数 a,b，替换两个网络 [a,b) 位置上的权值。

4.变异操作

对于网络中的每一个参数，生成一个随机数，如果小于 0.01，进行变异操作。

对于一次变异操作，可能变异的值为 x × 10y,x ∈ [0,1),y ∈ [0,1)。

3.5 结果分析

下面是迭代了 100 代后平均适应度和最好交叉熵的变化：

图 3: 平均适应度和最好交叉熵

可能是我没写对吧。。。种群的适应度没有什么太大的变化，可能是交叉操作过于简单，对于网络生成的权值影响较小。

对于遗传算法这块，没啥好说的，可能我运气不好，不适合这种运气算法吧。我感觉，这种遗传算法只能起辅助作用，作为训练的核心还是得好好考虑。

四、强化学习

4.1 问题描述

采用强化学习算法对上述人工神经网络模型进行学习，使得五子棋博弈程序的下棋水平不断提高。

4.2 方法描述

在 DQN 中采用的网络结构为三层卷积层，三层全连接层，输入为通道为 4 的 15x15 的棋盘，4 个通道按照落子顺序分别保存我方两步落子和敌方两步落子，如下：

图 4: 神经网络结构

可用的迭代方式为两种，一种是以当前的网络进行落子，直到下完一整局，随机抽取其中部分局面进行训练。还有一种就是每一步训练一次网络。在实际操作过程中，发现前一种 loss 无法收敛，猜测是因为每隔一盘训练一次，训练数据变化过大，导致网络无法有效地拟合。而后一种 loss 呈现出收敛的趋势，所以网络的训练方式采用后者。

对于网络的训练，采用了和随机落子，搜索落子，相同网络落子对抗的三种方式生成训练数据。最后虽然没有达到想要的结果，但 ai 的智能还是呈现上升的趋势。

4.3 原理描述

采用 Q-learning 算法，对于常规的 Q-learning 算法，核心公式为：

Q(S,A) ← (1 − α)Q(S,A) + α[R(S,A) + γ maxQ(S′,a)] a

通过不断迭代使 Q 值接近每一步的真实收益。当迭代稳定时，每一步选取最大 Q 值即可获得最优解。

Q-learning 算法中，关键就是 Q 值的计算，在计算 Q 值时，往往需要一张 Q 值表保存每一状态的所有动作对应的 Q 值。然而五子棋棋盘的状态数为 3225 ≈ 1e107。显然无法保存五子棋所有的状态。

这时候需要神经网络强大的拟合能力保存棋盘的状态。

对于神经网络的损失函数，定义如下：

通过计算网络的输出值与目标网络输出值的 MSE 计算 loss，然后进行反向传播，根据梯度更新权值。

4.4 步骤描述

关于 DQN 的实现代码位于 Python/DQN/ANN.py 文件中。

1.双网络

为了让网络能够收敛，使用双网络，一个为当前的落子网络，一个为目标网络，每隔 40 步，目标网络更新一次权值，将落子网络的权值复制到目标网络中。

2.经验回放

在网络训练的过程中，因为每一步落子都是连续有关联的，而训练数据要求独立分布，不然网络可能会记住这种关系导致效果不好，所以需要经验回放。

将所下的步骤存入记忆池中，每一步训练时，从记忆池中随机抽取一个 batch 大小的数据进行训练，打破了数据间的关联性。

3.奖励函数

首先说明，我并没有解决 DQN 过程中奖励稀疏的问题，还是采用开始的方法，获胜得 5 分，失败得-5 分，其余得 0 分的奖励方式。

这是在网络训练中最头疼的问题，alpha 系列都使用了蒙特卡洛树搜索作为奖励，很遗憾我没有写蒙特卡洛树搜索。

因为一开始我是直接将搜索 ai 作为训练对手，我的想法是，对于一个返回确定结果的对手，这样整个游戏就变成了一个确定的搜索树，只要在树的叶子节点也就是输赢节点标记奖励，路径上的奖励置为 0 就行，ai 就可以训练得到确定的 Q 值。

事实证明我的想法还是太过天真，DQN 训练过程中存在“稀疏奖励”问题。稀疏奖励问题是指 agent 探索的过程中难以获得正奖励，导致学习缓慢甚至无法进行学习的问题。如何解决奖励稀疏问题呢？一种方式是类似于人工生成评估函数，类似于 ai 形成活三，活四给予一定奖励，但这种方式太过生硬，实际上 ai 并没有自己学会这个博弈的诀窍。

为了不太过介入 ai 的学习过程，我的解决方案为给与每一个位置评分，越靠近中心分数越高。

但在实践过程中我发现，除了收敛速度有所提升，结果没有很大的变化，面对随机落子，还是按照固定的走法获胜，面对搜索 ai，还是随机落子。所以我认为这是一个失败的改动，所以采取了开始的奖励函数。

4.对于网络结构的处理

在开始的网络训练的时候，我直接输入的是当前棋面，结果网络的收敛速度非常慢，在查阅资料发现,aplha-go 的实现方式是保存我方 8 步和敌方 8 步的落子信息，可能这种连续的落子信息能够让网络找到有效的信息。修改之后网络的收敛速度确实有所提升。

4.5 结果分析

首先看一下整局训练和每一步训练的 loss 变化：

整局训练

每步训练

图 5: 训练方式不同的 loss 变化

可以看出整局训练的 loss 并没有收敛，而每步训练的方式 loss 呈现收敛的趋势。从实际测试中，我也看出，整局训练的落子还是杂乱无章，而每步训练已经会按照固定的取胜步骤进行落子。

在对战随机落子、搜索落子、自我训练的 ai 中，loss 变化分别如下：

随机落子

搜索落子

自我训练

图 6: 对战不同 ai 的 loss 变化

可以看出网络是逐渐收敛的。

上面已经说明了对于随机落子的 ai，网络训练得到的效果是比较好的。

而对于搜索落子的情况，虽然网络呈现收敛的趋势，但是实际效果并不是和搜索算法打得“有来有回”，而是和未训练时一样几步就输掉了。

在看了网络输出的每一步的 Q 值，我发现网络对于同一状态的每个动作的 Q 值大致相同，出现了类似反正怎么下都赢不了，随机下出一步算了的情况。稀疏奖励和一直找不到可行解的问题使得 ai 发现只要对每一个动作输出相同的权值，除了在结束时结果不符合以外，其他情况输出值和目标值大致相同，这就导致了出现了 loss 收敛，实际效果却不好的情况。

对于自我训练的 ai，loss 呈现收敛的趋势，而且相较于一开始双方随机乱下，训练后的 ai 落子更加集中，而且更加靠近中心位置，不会出现下在角落或者边缘的惊人举动。虽然对于依然存在“四子不连”的举动，但还是可以看出 ai 的智能有一定的提升。

对于奖励函数难以确定的情况，我想蒙特卡洛树搜索是更好的答案，它能让学习到的知识更加有效，而不会出现“奖励稀疏”的情况，一个好的奖励函数能让网络更加有效，更快地收敛。