大模型的后训练（post-training）方法

大模型的后训练（post-training）方法

后训练的主要目的是：

• 任务适配，从“通用知识”到“专用能力”，如拓展到金融领域
• 对齐人类偏好：从“普适化”到“个性化”，如人类价值观、情感需求对齐
• 增强特定能力：从“广覆盖”到“深聚焦”，如提高代码生成、数学推理的逻辑性
• 安全与合规性：从“无纪律”到“合法公民”，如根据法规调整色情信息的检索程度

与预训练的区别：

阶段	预训练（Pre-training）	后训练（Post-training）
目标	学习通用语言模式与世界知识	适配具体任务、对齐偏好、优化部署
数据	大规模无监督文本 （如网页、书籍）	小规模有监督数据 （如标注样本、偏好对）
方法	自回归/自编码语言模型	SFT、RLHF、蒸馏等
资源	需千卡级GPU集群训练数月	通常单卡或小规模集群，数小时至数天

一、SFT（Supervised Fine-tuneing）

通过在特定任务的数据上进行微调，提高模型在该任务上的性能

（一）全参数微调（Full Parameter Fine Tuning）

全参数微调涉及对模型的所有权重进行调整，以使其完全适应特定领域或任务。这种方法适用于拥有大量与任务高度相关的高质量训练数据的情况，通过更新所有参数来最大程度地优化模型对新任务的理解和表现。

（二）部分参数微调（Sparse Fine Tuning / Selective Fine Tuning）

部分参数微调策略仅选择性地更新模型中的某些权重，尤其是在需要保留大部分预训练知识的情况下。这包括：

• LoRA（Low-Rank Adaption）：通过向模型权重矩阵添加低秩矩阵来进行微调，减少需要学习的参数量，加快训练速度。
• P-tuning v2：是一种基于prompt tuning的方法，仅微调模型中与prompt相关的部分参数（例如，额外添加的可学习prompt嵌入），而不是直接修改模型主体的权重。
• QLoRA：可能是指Quantized Low-Rank Adaptation或其他类似技术，它可能结合了低秩调整与量化技术，以实现高效且资源友好的微调。

（三）冻结（Freeze）监督微调

在这种微调方式中，部分或全部预训练模型的权重被冻结（即保持不变不再训练），仅对模型的部分层（如最后一层或某些中间层）或新增的附加组件（如任务特定的输出层或注意力层）进行训练。这样可以防止预训练知识被过度覆盖，同时允许模型学习针对新任务的特定决策边界。

二、RLHF（Refinement Learning From Human Feedback）

基于人类反馈的强化学习是进行数据对齐的一种方式，可以避免暴力、色情等信息出现，也可以使其回答更符合人类喜好。

（一）PPO（Proximal Policy Optimization）–on-policy

• 收集人类反馈，人工标注数据，给出多个答案的排名
• 训练奖励模型（reward model, RM），（问题，答案）-> RM ->score标量
• 采用PPO强化学习优化需要优化的大模型${\pi }_{\theta }$，其奖励由上面的RM生成

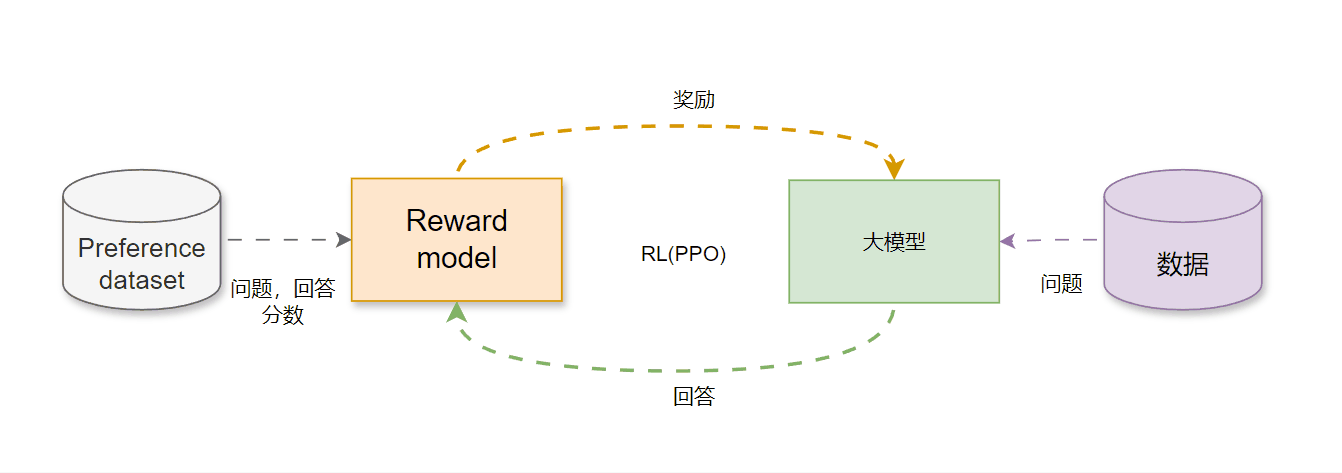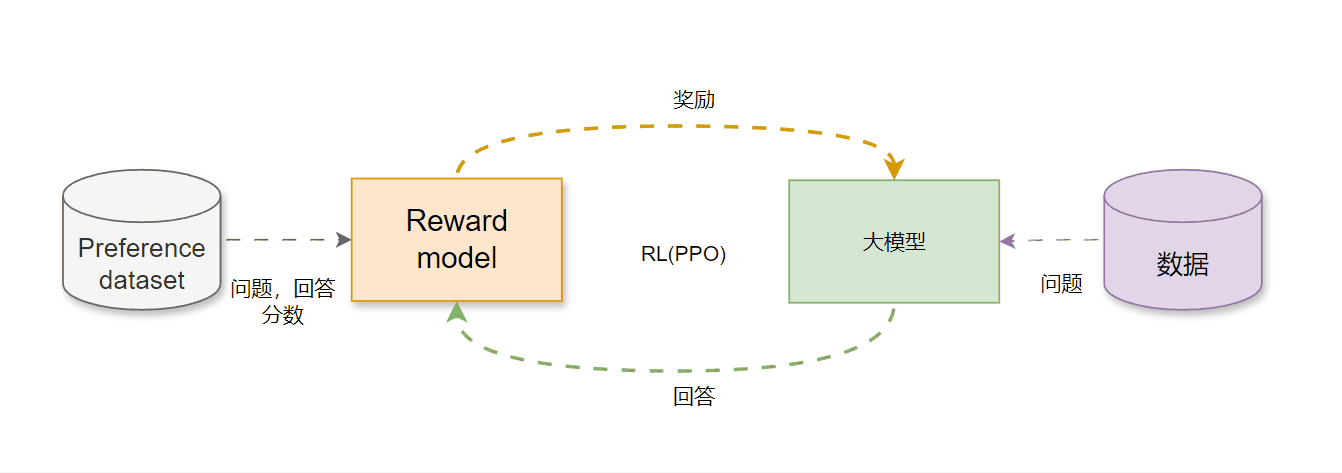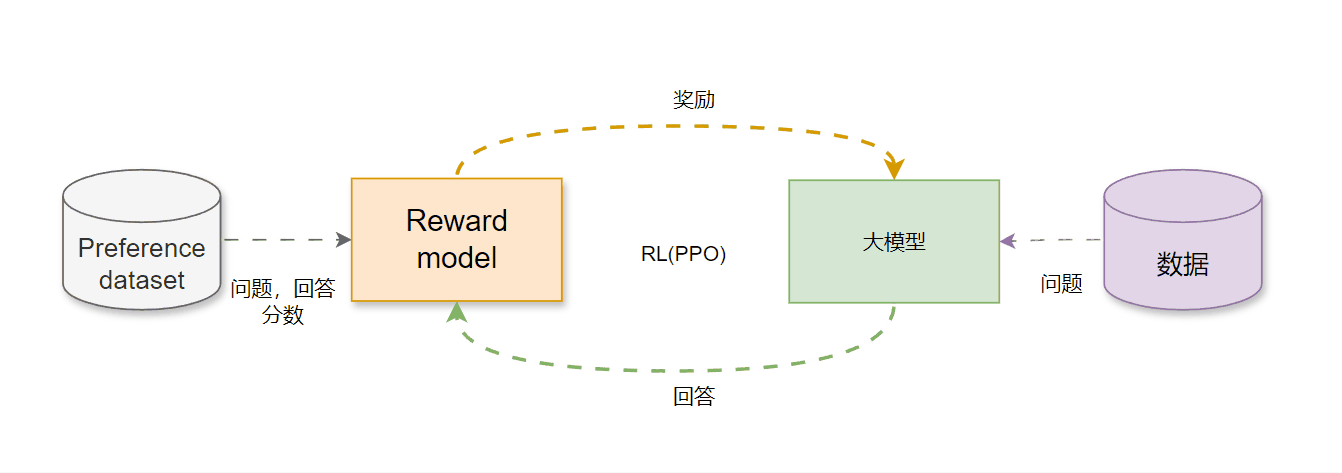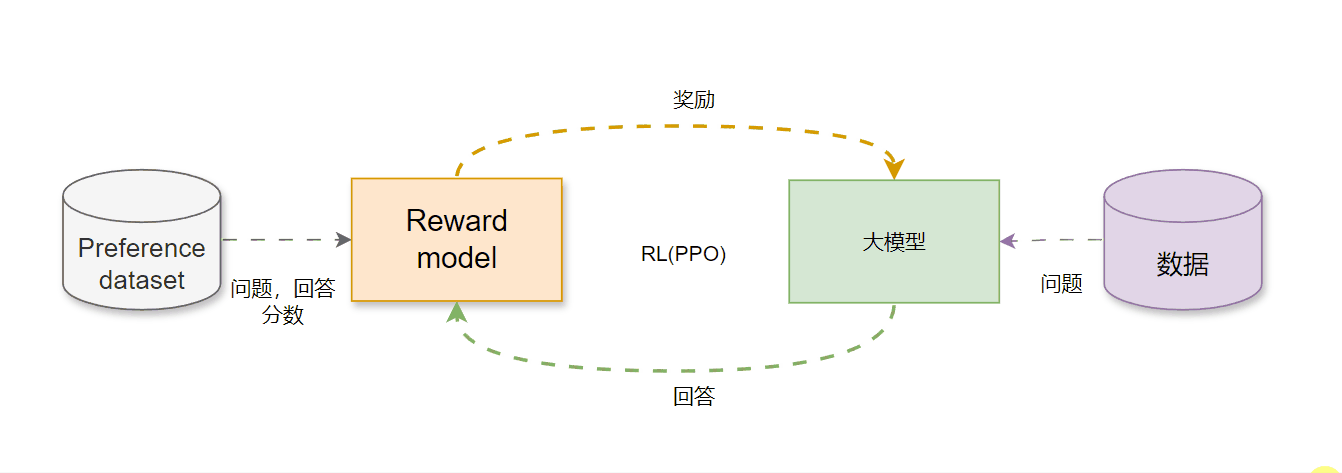
使用到该技术的有：Qwen，InstructGPT、GPT3.5、GPT4

def ppo_loss_with_gae_entropy(old_policy_logprobs, new_policy_logprobs, advantages, kl_penalty_coef, clip_epsilon, entropy_bonus_coef):
    """概念性 PPO 损失函数，带有 GAE 和熵奖励（简化版）。"""

    ratio = np.exp(new_policy_logprobs - old_policy_logprobs)  # 概率比

    # 剪切代理目标（限制策略变化）
    surrogate_objective = np.minimum(ratio * advantages, np.clip(ratio, 1 - clip_epsilon, 1 + clip_epsilon) * advantages)
    policy_loss = -np.mean(surrogate_objective)

    # KL 散度惩罚（保持接近旧策略）
    kl_divergence = np.mean(new_policy_logprobs - old_policy_logprobs)
    kl_penalty = kl_penalty_coef * kl_divergence

    # 熵奖励（鼓励探索）
    entropy = -np.mean(new_policy_logprobs)  # 简化版熵（概率越高 = 熵越低，取负值以最大化熵）
    entropy_bonus = entropy_bonus_coef * entropy

    total_loss = policy_loss + kl_penalty - entropy_bonus  # 减去熵奖励，因为我们希望*最大化*熵
    return total_loss

（二）DPO（Direct Preference Optimization) – off-policy

DPO避免了 PPO 的迭代 RL 循环。它直接基于人类偏好数据利用一个巧妙的损失函数对 LLM 进行优化。

• 收集人类偏好数据 D = { x ( i ) , y w ( i ) , y l ( i ) } i N D=\{{x^{(i)},y_w^{(i)},y_l^{(i)}}\}_i^N D={x(i),yw(i)​,yl(i)​}iN​,$x$是输入文本，$y_w$是人类标注的优选答案，$y_l$是次选答案
• 模型初始化，加载两个预训练模型，一个做策略模型（policy model）${\pi }_{\theta }$进行参数优化，一个做参考模型（reference model）参数固定用于计算KL散度约束，防止策略偏离原始分布。
• 使用任务分类思想直接优化策略模型的输出概率，通过策略与参考模型的对数概率差异隐式替代奖励函数
  • Bradley-Terry偏好模型：假设人类偏好概率与奖励值得sigmoid函数成正比
    • $P\left(y_w\succ y_l\mid x\right)=\frac{\exp \left(R\left(y_w,x\right)\right)}{\exp \left(R\left(y_w,x\right)\right)+\exp \left(R\left(y_l,x\right)\right)}$
  • 隐式奖励函数：奖励$R(y,x)$被定义为策略模型与参考模型得对数概率差异，$\beta$是温度参数，控制策略调整得幅度：
    • $R(y,x)=\beta \log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{\text{ref }}(y\mid x)}$
  • 损失函数：通过最大化偏好数据的对数似然，得到DPO损失函数
    • ${\mathcal{L}}_{\mathrm{DPO}}(\theta )=-{\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }\left(y_w\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_w\mid x\right)}-\beta \log \frac{{\pi }_{\theta }\left(y_l\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_l\mid x\right)}\right)\right]$
• 梯度下降训练

使用到该技术的模型有：Qwen2、Llama3

def dpo_loss(policy_logits_preferred, policy_logits_dispreferred, ref_logits_preferred, ref_logits_dispreferred, beta_kl):
    """概念性 DPO 损失函数（简化版——直接使用 logits）。"""

    # 1. 从 logits 中获取对数概率（当前和参考模型的首选和非首选响应）
    policy_logprob_preferred = F.log_softmax(policy_logits_preferred, dim=-1).gather(...)  # 提取首选响应中实际标记的对数概率
    policy_logprob_dispreferred = F.log_softmax(policy_logits_dispreferred, dim=-1).gather(...)  # 提取非首选响应中实际标记的对数概率
    ref_policy_logprob_preferred = F.log_softmax(ref_logits_preferred, dim=-1).gather(...)  # 同样适用于参考模型
    ref_policy_logprob_dispreferred = F.log_softmax(ref_logits_dispreferred, dim=-1).gather(...)

    # 2. 计算对数比率（使用对数概率——如前所述）
    log_ratio = policy_logprob_preferred - policy_logprob_dispreferred - (ref_policy_logprob_preferred - ref_policy_logprob_dispreferred)

    # 3. 偏好概率（Bradley-Terry 模型——隐式奖励信号）
    preference_prob = 1 / (1 + np.exp(-beta_kl * log_ratio))

    # 4. 二元交叉熵损失（直接优化策略）
    dpo_loss = -np.log(preference_prob + 1e-8)
    return dpo_loss

（三）GRPO（Group Relative Policy Optimization）

该方法由Deepseek v2中提出，是PPO的巧妙改造，其核心思想是通过组内相对奖励优化策略，避免传统PPO算法中价值函数模型的高计算开销。

特点

• 更瘦更快的PPO：通过同一状态下采样多个动作（输出），保留了核心的PPO理念，但去掉了价值函数（评论家）。
• 基于群体的优势估计（Group-Based Advantage Estimation，GRAE）：去掉价值函数后，通过大模型生成对同一prompt的一组答案来评估每个回答相对于组中其他回答的“好”程度。

步骤：

• 生成一组响应：对于每个提示，从LLM生成一组多个响应。
• 小组评分（奖励模式）：获得小组中所有回应的奖励分数。
• 计算组内相对优势（GRAE -组内比较）：通过将每个响应的奖励与组内平均奖励进行比较来计算优势。在团队内部规范奖励以获得优势。
• 优化策略（带有GRAE的类似ppo的目标）：使用ppo风格的目标函数更新LLM的策略，但使用这些组相对优势。

$L(\theta )=\mathbb{E}\left[\frac{{\pi }_{\theta }(a\mid s)}{{\pi }_{\text{old }}(a\mid s)}{A}_{\text{rel }}(s,a)\right]-\beta \mathrm{KL}\left({\pi }_{\theta }\Vert {\pi }_{\text{old }}\right)$

def grae_advantages(rewards):
    """概念性组相对优势估计（结果监督）。"""
    mean_reward = np.mean(rewards)
    std_reward = np.std(rewards)
    normalized_rewards = (rewards - mean_reward) / (std_reward + 1e-8)
    advantages = normalized_rewards  # 对于结果监督，优势 = 归一化奖励
    return advantages


def grpo_loss(old_policy_logprobs_group, new_policy_logprobs_group, group_advantages, kl_penalty_coef, clip_epsilon):
    """概念性 GRPO 损失函数（对一组响应取平均）。"""
    group_loss = 0
    for i in range(len(group_advantages)):  # 遍历组内的每个响应
        advantage = group_advantages[i]
        new_policy_logprob = new_policy_logprobs_group[i]
        old_policy_logprob = old_policy_logprobs_group[i]

        ratio = np.exp(new_policy_logprob - old_policy_logprob)
        clipped_ratio = np.clip(ratio, 1 - clip_epsilon, 1 + clip_epsilon)
        surrogate_objective = np.minimum(ratio * advantage, clipped_ratio * advantage)
        policy_loss = -surrogate_objective

        kl_divergence = new_policy_logprob - old_policy_logprob
        kl_penalty = kl_penalty_coef * kl_divergence
        group_loss += (policy_loss + kl_penalty)  # 累加组内每个响应的损失

    return group_loss / len(group_advantages)  # 对组内损失取平均

使用到该技术的模型有：DeepSeek AI、Qwen2.5

三者对比

特性	PPO	DPO	GRPO
Reward Model	神经网络显式学习	隐式学习	隐式学习
价值函数	✅单独神经网络	❎	❎
训练循环复杂度	更复杂（RL loop、Critic training）	简单（no RL loop，直接优化）	简单的RL训练（组采样、没有critic）
优势估计	GAE（使用价值函数）	不相关（隐式奖励）	GRAE
计算效率	低	更高	高
应用难度	更高	简单	高
相关模型	Qwen，InstructGPT、GPT3.5、GPT4	Qwen2、Llama3	DeepSeek AI、Qwen2.5