当前位置：首页 > news >正文

机器学习（神经网络基础篇）——个人理解篇6(概念+代码)

news 来源：原创 2025/4/21 7:49:50

1 在声明一个类中，构建一个属于类的函数，前面为什要加上“self”？

就像下面这一串代码：

 class TwoLayerNet:def __init__(self, input_size, hidden_size, output_size,weight_init_std=0.01):# 
初始化权重self.params = {}self.params['W1'] = weight_init_std * \np.random.randn(input_size, hidden_size)self.params['b1'] = np.zeros(hidden_size)self.params['W2'] = weight_init_std * \np.random.randn(hidden_size, output_size)self.params['b2'] = np.zeros(output_size)def predict(self, x):W1, W2 = self.params['W1'], self.params['W2']b1, b2 = self.params['b1'], self.params['b2']a1 = np.dot(x, W1) + b1z1 = sigmoid(a1)a2 = np.dot(z1, W2) + b2y = softmax(a2)return y

解释：

在Python中，self 是一个指向当前类实例自身的引用参数，它的作用类似于“我”或“这个对象”。它的存在是为了让类的方法（函数）能够访问和操作这个实例的属性（变量）和其他方法。

专业解释：

1 访问实例属性
在 predict 方法中，你需要访问当前实例的权重参数 self.params['W1']、self.params['b1'] 等。没有 self，方法就不知道去哪里找这些参数。
2 区分不同实例
如果有多个神经网络实例（比如 net1 和 net2），它们的权重参数是独立的。通过 self，每个实例的方法只会操作自己的参数，不会互相干扰。

通俗解释：
想象你有一个机器人（类 TwoLayerNet），它身上有多个按钮（属性如 params）和功能（方法如 predict）。当你按下某个功能按钮时，机器人需要知道：“这个功能是针对 我自身 的哪些属性操作的？”这时 self 就是告诉机器人：“操作的是当前这个机器人自己的按钮，而不是其他机器人的。”

总结：self 是类方法的“自我标识符”，让方法知道应该操作哪个实例的数据。没有它，类的方法就无法区分不同实例的属性。

2 神经网络中的参数优化，你知道哪些？有什么优缺点？（纯个人总结）

所谓优化，实质上是找使得损失函数的值最小的一组参数。举一个生活中的例子：

2.1 用调热水澡水温类比神经网络参数优化

想象你正在调整淋浴的冷热水龙头，目标是找到 最舒适的水温。这个过程与神经网络的参数优化惊人地相似：

1. 初始状态（参数初始化）

场景：第一次打开淋浴，随机拧动冷热龙头（初始权重和偏置随机设置）。
结果：水温要么太冷（预测错误），要么太烫（损失函数值大）。

2. 试水温（前向传播）

动作：伸手试水温，感受冷热程度。
对应：
- 输入数据 = 当前冷热水比例（参数）
- 输出结果 = 实际水温（预测值）
- 目标 = 理想水温（标签）
- 误差 = 水温偏差（损失函数值）

3. 调整龙头（反向传播与梯度下降）

冷热不均（计算梯度）：
- 若水太冷 → 需要更多热水（梯度指向增加热水权重的方向）。
- 若水太热 → 需要更多冷水（梯度指向减少热水权重的方向）。
- 调整幅度 = 手拧龙头的力度（学习率）。
具体操作：
- 微调热水龙头开大一点（参数更新公式：W = W - 学习率 × 梯度）。
- 下次再试水温（下一轮训练）。

4. 反复调试（迭代优化）

过程：
太冷 → 加热水 → 试水 → 太烫 → 减热水 → 试水 → 接近舒适 → 微调...
对应：
通过多次迭代（epoch），参数（冷热水比例）逐渐收敛到最佳值（损失函数最小化）。

5. 成功（模型收敛）

结果：水温稳定在理想温度（模型准确预测）。
关键因素：
- 学习率：手拧龙头的幅度太大（学习率高）→ 水温反复震荡；幅度太小（学习率低）→ 调整过慢。
- 耐心（迭代次数）：足够多的调试次数才能找到平衡点。

2.2 SGD（随机下降）介绍

1 核心公式：

这里把需要更新的权重参数记为W，把损失函数关于W的梯度记为。 η表示学习率，实际上会取0.01或0.001这些事先决定好的值。上式中的←表示用右边的值更新左边的值。（可以理解为朝向梯度下降的方向前进）

2 SGD缺点：

首先来求的最值问题。

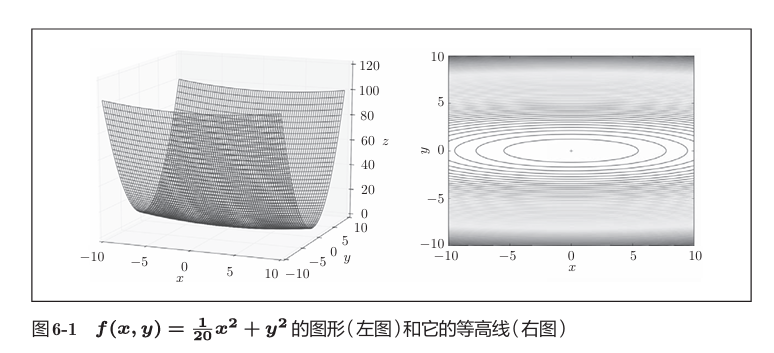
左图表示的函数是向x轴方向延伸的“碗”状函数。右图是等高线呈向x轴方向延伸的椭圆状。

此函数对应的梯度如下图：

这个梯度的特征是，y轴方向上大，x轴方向上小。换句话说，就是y轴方向的坡度大，而x轴方向的坡度小。假设从（x , y ）=（-7, 2）处（初始值）开始搜索，结果如下图所示：

如图，虽然最后能找到“最优点”，但是过程很曲折，，SGD呈“之”字形移动。这是一个相当低效的路径，在Y轴上跨度比较大，但是在水平方向上看，每次平移的：“步伐”总是很小。

为了改正SGD的缺点，下面将介绍Momentum、AdaGrad、Adam这3 种方法来取代SGD。

2.3 　Momentum（同SGD相比，引入了阻力下的初始速度）

Momentum是“动量”的意思，和物理有关。

1 我个人的理解：

将二维空间图像的梯度进行正交分解，在梯度跨度大的方向（比如Y轴）对梯度的跨度进行适当的“动态调整”，在梯度跨度小的方向（比如X轴）对梯度的跨度施加外力作用，“迫使”梯度跨度逐渐增加。

2 核心公式：

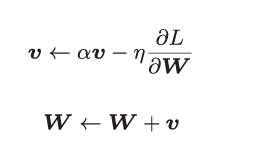
和前面的SGD一样，W表示要更新的权重参数，表示损失函数关于W的梯度，η表示学习率。这里新出现了一个变量v，对应物理上的速度。

例如下图：

αv这一项，在物体不受任何力时，该项承担使物体逐渐减速的任务（α设定为0.9之类的值），对应物理上的地面摩擦或空气阻力。

class Momentum:def __init__(self, lr , moment):self.lr = lrself.moment = momentself.v = Nonedef update (self, para , grad):if self.v is None:self.v = {}for key , val in para.items():self.v[key] = np.zeros_like(val)for key in para.keys():para[key] = self.moment * self.v[key] - self.lr - grad[key]para[key] =+ self.v[key]

实例变量v会保存物体的速度。初始化时，v中什么都不保存，但当第一次调用update()时，v会以字典型变量的形式保存与参数结构相同的数据。

假设采用Momentum解决函数最优化的问题，相应的优化路径如下：

和SGD相比，我们发现 “之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比，可以更快地朝x轴方向靠近，减弱“之”字形的变动程度。

2.4 AdaGrad

在神经网络的学习中，学习率（数学式中记为η）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。

有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。

AdaGrad会为参数的每个元素适当地调整学习率。

1 核心公式：

和前面的SGD一样，W表示要更新的权重参数，表示损失函数关于W的梯度，η表示学习率。这里新出现了变量h，它保存了以前的所有梯度值的平方和（表示对应矩阵元素的乘法）。然后，在更新参数时，通过乘以，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。

AdaGrad代码实现过程：

class AdaGrad:def __init_(self, lr = 0.01):self.lr = lrself.h = Nonedef update(self, para, grad):if self.h is None:self.h = {}for key, val in para.items():self.h[key] = np.zeros_like(val)for key in para.keys():self.h[key] += grad[key] * grad[key]para[key] -= self.lr * grad[key] / (np.sqrt(self.h[key]) + 1e-7)

假设采用AdaGrad解决函数最优化的问题，相应的优化路径如下：