无人船 | 图解基于PID控制的路径跟踪算法(以全驱动无人艇WAMV为例)
目录
- 1 PID控制基本原理
- 2 基于全驱动运动学的PID控制
- 3 跟踪效果分析
1 PID控制基本原理
PID控制是一种常用的经典控制算法,其应用背景广泛,例如
- 工业自动化控制:温度控制、压力控制、流量控制、液位控制等过程控制系统多采用PID闭环,可以帮助维持系统参数在设定值附近,以提高生产过程的稳定性和效率;
- 机械工程:PID算法可用于实现精确的运动控制,包括控制位置、速度和力。这包括机器人控制、电机控制、汽车巡航控制等;
- 农业自动化:PID算法可用于控制温室环境,包括温度、湿度和光照,以促进植物的生长和提高农业生产;
- …
PID代表比例(Proportional)、积分(Integral)和微分(Derivative),它通过根据误差信号的大小和变化率来调整控制器的输出,以使系统的输出尽可能接近期望值,其控制框图如下所示

连续型PID控制律如下
u ( t ) = K p e ( t ) + K i ∫ t 0 t e ( τ ) d τ + K d e ˙ ( t ) u\left( t \right) =K_pe\left( t \right) +K_i\int_{t_0}^t{e\left( \tau \right) \mathrm{d}\tau}+K_d\dot{e}\left( t \right) u(t)=Kpe(t)+Ki∫t0te(τ)dτ+Kde˙(t)
其中 K p K_p Kp、 K i K_i Ki、 K d K_d Kd分别称为比例、积分与微分增益系数
位置式离散型PID控制律如下
u ( k ) = K p e ( k ) + K i ∑ i = 0 k e ( i ) Δ t + K d ( e ( k ) − e ( k − 1 ) ) / Δ t u\left( k \right) =K_pe\left( k \right) +K_i\sum_{i=0}^k{e\left( i \right) \varDelta t}+K_d{{\left( e\left( k \right) -e\left( k-1 \right) \right)}/{\varDelta t}} u(k)=Kpe(k)+Kii=0∑ke(i)Δt+Kd(e(k)−e(k−1))/Δt
由于位置式PID算法需要计算累计偏差,占用存储单元,可以通过
u ( k ) − u ( k − 1 ) u\left( k \right) -u\left( k-1 \right) u(k)−u(k−1)
计算增量式PID控制律
Δ u ( k ) = K p Δ e ( k ) + K i e ( k ) Δ t + K d ( Δ e ( k ) − Δ e ( k − 1 ) ) / Δ t \varDelta u\left( k \right) =K_p\varDelta e\left( k \right) +K_ie\left( k \right) \varDelta t+K_d{{\left( \varDelta e\left( k \right) -\varDelta e\left( k-1 \right) \right)}/{\varDelta t}} Δu(k)=KpΔe(k)+Kie(k)Δt+Kd(Δe(k)−Δe(k−1))/Δt
其中
Δ u ( k ) = u ( k ) − u ( k − 1 ) Δ e ( k ) = e ( k ) − e ( k − 1 ) \varDelta u\left( k \right) =u\left( k \right) -u\left( k-1 \right) \\ \varDelta e\left( k \right) =e\left( k \right) -e\left( k-1 \right) Δu(k)=u(k)−u(k−1)Δe(k)=e(k)−e(k−1)
更多PID控制理论请参考控制原理 | PID控制的三个参数如何影响控制效果?(附参数整定方法)
在基于PID的局部路径规划中,希望USV能快速跟踪上预设的轨迹,设误差量为 e k e_k ek。 e k e_k ek可以根据实际的控制目标进行选择,例如线速度误差、角速度误差、轨迹跟踪误差等
2 基于全驱动运动学的PID控制
全驱动无人船路径跟踪控制通过三自由度独立调节实现精确轨迹跟随,其核心在于建立基于运动学模型的PID多环控制架构。系统将船体运动解耦为纵向推进、横向位移与航向调整三个正交自由度,每个自由度采用独立的PID控制器生成推力指令,最终通过推力分配矩阵将虚拟控制量转化为各推进器的实际推力输出,形成闭环反馈控制回路。
根据LOS制导律,当船体采用 ψ = ψ d \psi =\psi _d ψ=ψd制导时可使横向误差收敛为零,因此设计基于艏向误差
e ψ = ψ d − ψ e_{\psi}=\psi _d-\psi eψ=ψd−ψ
的航向PID控制律
τ r = K p ψ e ψ + K i ψ ∫ e ψ d t + K d ψ d e ψ d t \tau _r=K_{p}^{\psi}e_{\psi}+K_{i}^{\psi}\int{e_{\psi}\mathrm{d}t}+K_{d}^{\psi}\frac{\mathrm{d}e_{\psi}}{\mathrm{d}t} τr=Kpψeψ+Kiψ∫eψdt+Kdψdtdeψ
其中误差量作用于USV艏转力矩以控制方向。
接着,设计基于期望速度 u d u_d ud与当前速度误差
e u = u d − u 2 + v 2 e_u=u_d-\sqrt{u^2+v^2} eu=ud−u2+v2
的纵向速度PID控制律
τ u = K p u e u + K i u ∫ e u d t + K d u d e u d t \tau _u=K_{p}^{u}e_u+K_{i}^{u}\int{e_u\mathrm{d}t}+K_{d}^{u}\frac{\mathrm{d}e_u}{\mathrm{d}t} τu=Kpueu+Kiu∫eudt+Kdudtdeu
通过欠驱动推力分配关系即可得到实际控制量
[ τ b , l τ b , r ] = [ 1 1 − D D ] − 1 [ τ u τ r ] \left[ \begin{array}{c} \tau _{b,l}\\ \tau _{b,r}\\\end{array} \right] =\left[ \begin{matrix} 1& 1\\ -D& D\\\end{matrix} \right] ^{-1}\left[ \begin{array}{c} \tau _u\\ \tau _r\\\end{array} \right] [τb,lτb,r]=[1−D1D]−1[τuτr]
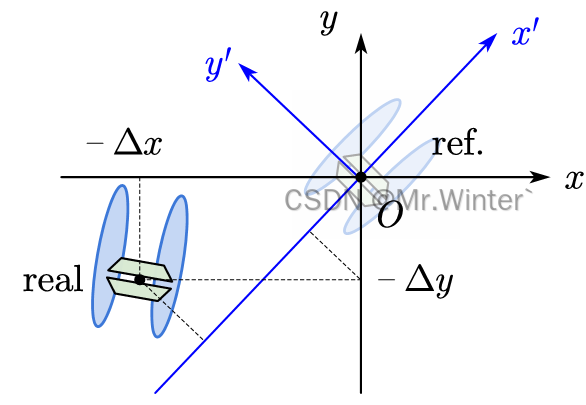
考虑到全驱动无人艇具有额外的横向螺旋桨,且该桨产生的横漂力不与前进和转向行为耦合,因此可以根据如图所示的几何关系设计独立的基于横向误差
e l a t e r a l = ( y d − y ) cos ψ − ( x d − x ) sin ψ e_{\mathrm{lateral}}=\left( y_d-y \right) \cos \psi -\left( x_d-x \right) \sin \psi elateral=(yd−y)cosψ−(xd−x)sinψ
的横向误差控制律
τ b , m = K p l a t e r a l e l a t e r a l + K i l a t e r a l ∫ e l a t e r a l d t + K d l a t e r a l d e l a t e r a l d t \tau _{b,m}=K_{p}^{\mathrm{lateral}}e_{\mathrm{lateral}}+K_{i}^{\mathrm{lateral}}\int{e_{\mathrm{lateral}}\mathrm{d}t}+K_{d}^{\mathrm{lateral}}\frac{\mathrm{d}e_{\mathrm{lateral}}}{\mathrm{d}t} τb,m=Kplateralelateral+Kilateral∫elateraldt+Kdlateraldtdelateral
3 跟踪效果分析
定性测试结果:

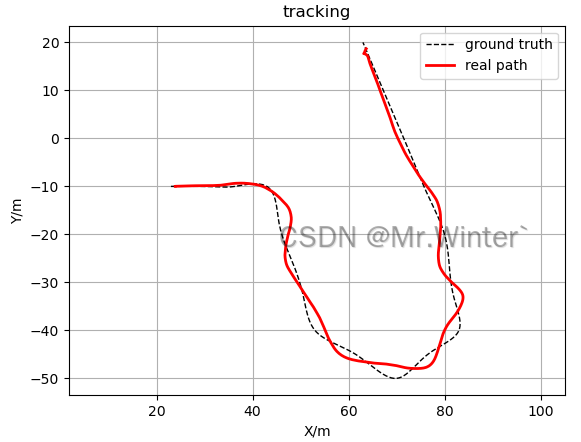
在考虑水动力、风力等真实干扰的情况下,跟踪轨迹如下所示,定量测试结果为:
- 平均跟踪误差:0.983 m
- 最大跟踪误差:2.726 m
- 最小跟踪误差:0.008 m
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
