无人船 | 图解基于PID控制的路径跟踪算法(以欠驱动无人艇Otter为例)
目录
- 1 PID控制的三大组成
- 1.1 比例控制作用
- 1.2 积分控制作用
- 1.3 微分控制作用
- 2 基于欠驱动运动学的PID控制
- 3 跟踪效果分析
1 PID控制的三大组成
PID控制律的定量表达请参考无人船 | 图解基于PID控制的路径跟踪算法(以全驱动无人艇WAMV为例),本文进一步介绍PID每个部分的作用

1.1 比例控制作用
比例控制根据误差信号的大小来产生控制器的输出
比例控制通过将误差信号与一个比例增益相乘来生成控制输出。增强比例控制作用 K p K_p Kp对系统性能的影响主要为
- 对瞬态性能的影响:加快动态响应速度,提高系统快速性;加快阻尼振荡频率,延长系统调节时间,同时增大超调量,降低系统平稳性。
- 对稳态性能的影响:(增大开环增益)减小系统稳态误差,提高系统控制精度;降低系统稳定裕度,不利于系统稳定性。
从时域角度看,如图所示根轨迹图,在增大 K p K_p Kp的过程中,系统自然频率增大,动态响应加快;阻尼频率增大,增加阻尼振荡次数;系统阻尼比减小,增大超调; K p K_p Kp过大会使闭环极点进入右半平面造成系统失稳

从频域特性角度看,增大 K p K_p Kp相当于抬高系统幅频特性,增大穿越频率(因此增加闭环带宽,加快动态响应),降低相角裕度(因此减小系统阻尼)。
如图所示为调节 K p K_p Kp对二阶系统响应的影响

1.2 积分控制作用
积分控制根据误差信号的累积量来产生控制器的输出
积分控制通过将误差信号与一个积分增益相乘,并将累积的误差值相加来生成控制输出。增强积分控制作用 对系统性能的影响主要为:
- 对系统瞬态性能的影响:加快动态响应速度,提高系统快速性;加快阻尼振荡频率,延长系统调节时间,同时增大超调量,降低系统平稳性。
- 对系统稳态性能的影响:(增加系统型数)消除稳态误差,提高系统控制精度;引入滞后相角,降低系统稳定裕度,不利于系统稳定性。
必须指出,积分控制与比例控制改善系统稳态性能的本质不同,后者属于有差控制,即只有存在误差 e e e,控制器才有输出,因此比例控制只能减小误差却不能完全消除误差;前者属于无差控制,当系统存在误差 e e e时,控制器通过积分作用消除误差,此时控制器保持一个为消除误差而产生的输出值
积分控制的无差性虽然提升了稳态性能,但一方面引入滞后相角牺牲了动态性能,另一方面产生了积分饱和问题。积分饱和指控制器为调节误差不断增大修正输出值,导致后续组件超过物理极限进入非线性环节,使控制器失去调节作用,引发严重超调的现象。例如在积分控制下,某管路阀门开度被调节至最大,此后产生误差虽然使控制器进一步增大输出,但阀门已不具有调节作用,系统失去控制能力。为解决该问题,需要引入抗积分饱和的控制算法。
如图所示为调节 对二阶系统响应的影响

1.3 微分控制作用
微分控制根据误差信号的变化率来产生控制器的输出
微分控制通过将误差信号的变化率与一个微分增益相乘来生成控制输出。增强微分控制作用 对系统性能的影响主要为:
- 对系统瞬态性能的影响:在一定范围内,加快动态响应速度,提高系统快速性;同时减小超调量,提高系统平稳性。超过该范围,微分控制仍会增大超调。
- 对系统稳态性能的影响:(增大开环增益)减小稳态误差,提高系统控制精度;引入超前相角,提高系统稳定裕度,有利于系统稳定性,但过强的微分控制仍会超出系统裕度破坏稳定性;放大高频噪声,削弱系统抗噪能力。
需要注意,单独的微分控制器由于带宽无穷大,物理不可实现,因此实用的微分控制环节总是伴随着比例控制或积分控制。由于在纯滞后时间内系统参数不变化,因此微分控制对纯滞后环节无效。
如图所示为调节 K d K_d Kd对二阶系统响应的影响

2 基于欠驱动运动学的PID控制
欠驱动无人船路径跟踪控制通过二自由度独立调节实现精确轨迹跟随,其核心在于建立基于运动学模型的PID多环控制架构。系统将船体运动解耦为纵向推进与航向调整两个正交自由度,每个自由度采用独立的PID控制器生成推力指令,最终通过推力分配矩阵将虚拟控制量转化为各推进器的实际推力输出,形成闭环反馈控制回路。
根据LOS制导律,当船体采用 ψ = ψ d \psi =\psi _d ψ=ψd制导时可使横向误差收敛为零,因此设计基于艏向误差
e ψ = ψ d − ψ e_{\psi}=\psi _d-\psi eψ=ψd−ψ
的航向PID控制律
τ r = K p ψ e ψ + K i ψ ∫ e ψ d t + K d ψ d e ψ d t \tau _r=K_{p}^{\psi}e_{\psi}+K_{i}^{\psi}\int{e_{\psi}\mathrm{d}t}+K_{d}^{\psi}\frac{\mathrm{d}e_{\psi}}{\mathrm{d}t} τr=Kpψeψ+Kiψ∫eψdt+Kdψdtdeψ
其中误差量作用于USV艏转力矩以控制方向。
接着,设计基于期望速度 u d u_d ud与当前速度误差
e u = u d − u 2 + v 2 e_u=u_d-\sqrt{u^2+v^2} eu=ud−u2+v2
的纵向速度PID控制律
τ u = K p u e u + K i u ∫ e u d t + K d u d e u d t \tau _u=K_{p}^{u}e_u+K_{i}^{u}\int{e_u\mathrm{d}t}+K_{d}^{u}\frac{\mathrm{d}e_u}{\mathrm{d}t} τu=Kpueu+Kiu∫eudt+Kdudtdeu
通过欠驱动推力分配关系即可得到实际控制量
[ τ b , l τ b , r ] = [ 1 1 − D D ] − 1 [ τ u τ r ] \left[ \begin{array}{c} \tau _{b,l}\\ \tau _{b,r}\\\end{array} \right] =\left[ \begin{matrix} 1& 1\\ -D& D\\\end{matrix} \right] ^{-1}\left[ \begin{array}{c} \tau _u\\ \tau _r\\\end{array} \right] [τb,lτb,r]=[1−D1D]−1[τuτr]
3 跟踪效果分析
定性测试结果:
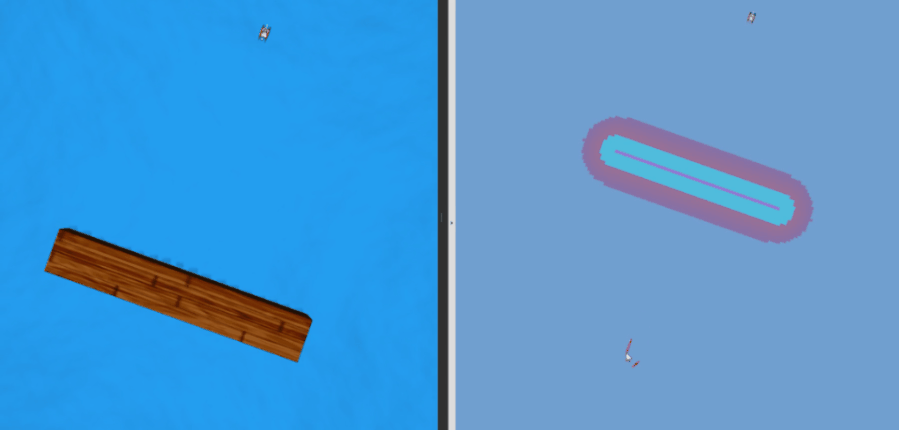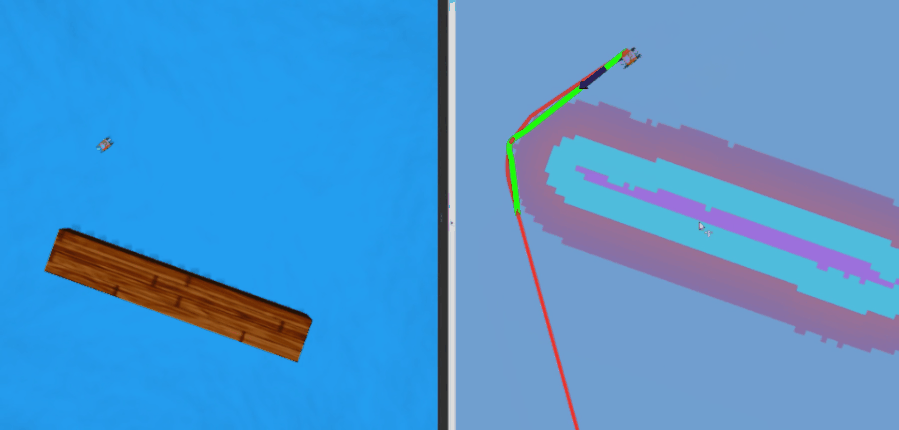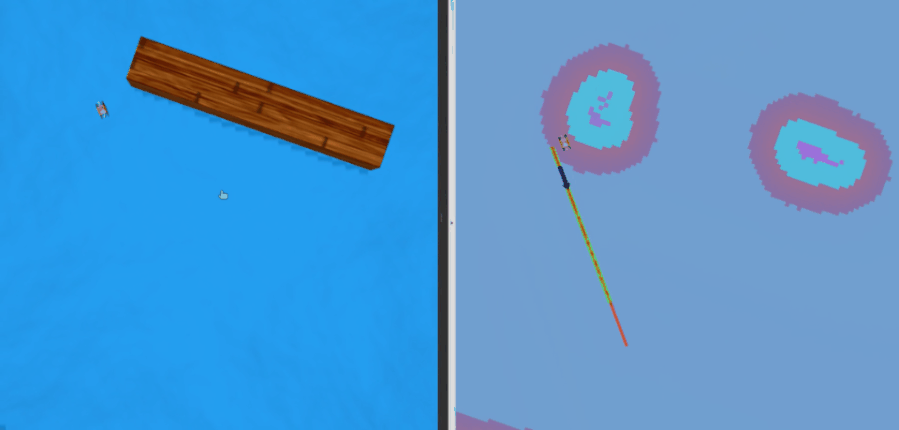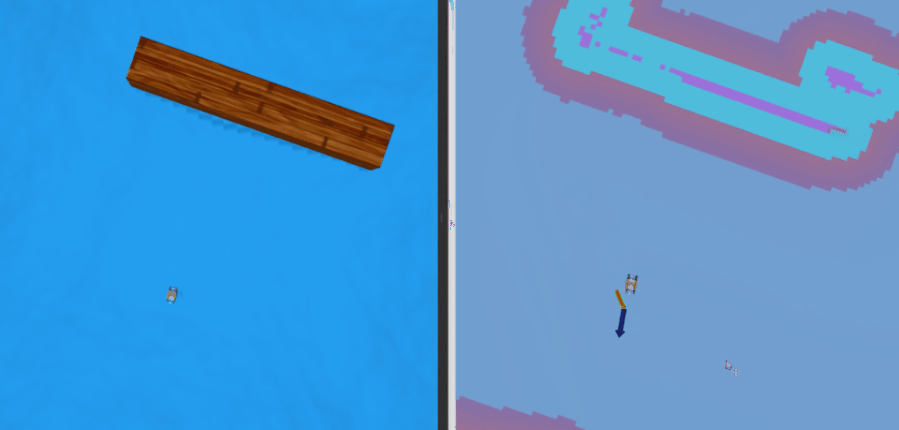
在考虑水动力、风力等真实干扰的情况下,跟踪轨迹如下所示,定量测试结果为:
- 平均跟踪误差:0.366 m
- 最大跟踪误差:0.580 m
- 最小跟踪误差:0.015 m

