计算机图形学(一):基础
# 基础概念
-
左/右手坐标系
左手坐标系和右手坐标系之间的差异就是某一个坐标轴的方向取反,可以是X轴,可以是Y轴,也可以是Z轴。

· OpenGL中的坐标系大都是右手坐标系;
· OSG使用右手坐标系;
· Unreal Engine采用左手坐标系;
· DirectX采用左手坐标系;
🟠右手坐标系:从旋转轴的上方看下,逆时针方向为旋转正方向;
🟡左手坐标系:从旋转轴的上方看下,顺时针方向为旋转正方向;
其他:在查看glm或者DirectXMath这类库时,通常可以在其中发现同一个函数有LH和RH两个版本 [链接]
扩展:左右手系转换
- 链接:左右手坐标系转换-CSDN博客
-
行主序/列主序存储

· OpenGL中的矩阵元素是采用列主序存储;
· OSG是采用行主序存储;
· Unreal Engine采用行主序存储;
· Direct3D 采用行主序存储;
示例:当要存储如图的矩阵信息时:

在OpenGL中的写法:
GLfloat m[] = {1.0f, 0.0f, 0.0f, 0.0f, // 对应 X列0.0f, 1.0f, 0.0f, 0.0f, // 对应 Y列0.0f, 0.0f, 1.0f, 0.0f, // 对应 Z列tx, ty, tz, 1.0f}; // 平移列在OSG中的写法:
osg::Matrixd matrix(1.0f, 0.0f, 0.0f, tx,0.0f, 1.0f, 0.0f, ty,0.0f, 0.0f, 1.0f, tz,0.0f, 0.0f, 0.0f, 1.0f
);-
向量/矩阵+左乘/右乘
或者也可以叫做“前乘“(pre-multiply)与”后乘“(post-multiply)。
行向量左乘还是右乘是矩阵乘法规则的限制,行向量只能左乘,而列向量只能右乘矩阵;

· 有人说OpenGL都是右乘、OSG都是左乘从结论上来说是对的,但是这和OpenGL以及OSG本身并没有半点关系,这只是矩阵乘法的定义 [链接]。
所谓矩阵左乘,其实就是矩阵放到乘号左边乘的意思;所谓矩阵右乘,其实就是矩阵放到乘号右边乘的意思(向量同理)。
-
点积与叉积
点积代数意义:
点积几何意义:
叉积代数意义:(注:结果是一个向量
叉积几何意义:
-
线性变换、正交变换、仿射变换
🟢 线性变换:线性变换是通过矩阵乘法来实现的,如旋转、缩放。
🔵 正交变换:线性变换的一种,它从实内积空间V映射到V自身,且保证变换前后内积不变
内积(a,b),对正交变换T,有(a,b)=(T(a),T(b))
🟣 仿射变换:仿射变换不能光通过矩阵乘法来实现,还得有加法(但可以在高维度通过线性变换实现低维度的仿射变换),如平移。“仿射变换”就是:“线性变换”+“平移”(旋转、缩放、平移);

链接:如何通俗地讲解「仿射变换」? - 知乎
链接:图形学中的基本变换(Basic Transforms)
-
矩阵变换
以OpenGL为例的矩阵形式
(一)平移

(二)缩放

(三)旋转
注意:下述旋转矩阵的中心点是(0,0),当旋转中心点不同时,旋转矩阵也会变化。
反向旋转的矩阵恰等于其转置矩阵(可通过cos(−θ) = cos(θ)和sin(−θ) = −sin(θ)验证)
- 绕Z轴旋转

- 绕X轴旋转

- 绕Y轴旋转

扩展:绕任意点的旋转矩阵
![]()
当我们需要进行绕任意点旋转时,可以把这种情况转换到绕原点的旋转,思路如下 [链接]:
- 1. 首先将旋转点移动到原点处;
- 2. 执行绕原点的旋转;
- 3. 再将旋转点移回到原来的位置;

即:

基的转换
已知一个向量v在一个基Q之中的坐标v',以及另外一个基R,我们可以通过公式来计算在R基中的坐标v'':

所以在已知两个基的情况下,可以得到基A的向量v在基B的坐标表示(反过来也行)。
若Q是和参考系相同的坐标系(3D编程中大多数情况下如此),比如世界坐标系,则Q是一个单位矩阵I,所以当已知Q下的坐标v',计算其在R基下的坐标v'':
![]()
例如:我们可以以相机位置作为坐标原点建立一个参考系,从世界空间变换到相机空间,即把物体从世界坐标系变换到相机为原点的相机坐标系(反过来也行)。

这里涉及两个坐标系:世界坐标系和相机坐标系,它们之间通过平移旋转变换可以实现重合。
UVN系统
UVN系统本质上就是在世界坐标参考系下,构成相机(世界坐标参考系下)的三个基向量,分别代表相机的右向(x)、上向(y)和后方(z)(左手系则为前方),也就是确定了在x轴、y轴和z轴三个标准正交基,构成了一个相机坐标系(相机处于世界坐标原点),这本质上就是一个旋转矩阵的构成。
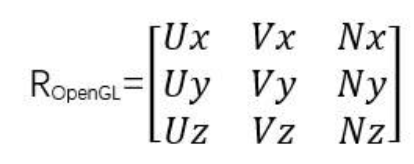
根据相机位置eye和观察目标center,可以求出向量N(右手系):N = eye - center;
📌 注:在左手系中 N = center - eye;
为了建立UVN系,除了①相机位置eye;②观察目标center;还需要知道③相机的正上方向量up;通过N和up叉乘,得到向量V,V = N × Up;在保证了三个向量都得到标准化(单位化)之后,就已经获得了UVN相机模型的三个基向量。
链接:https://zhuanlan.zhihu.com/p/561394626
示例:OSG中的代码
Vec3d lv( center - eye ); // 计算前向向量Vec3d f( lv ); // 前向向量
f.normalize();
Vec3d s( f^up ); // 计算右向向量,up一般取osg::Vec3d(0., 1., 0.),注意叉积不符合交换律
s.normalize();
Vec3d u( s^f ); // 计算上向向量
u.normalize();osg::Matrixd rotation_matrix(s[0], u[0], -f[0], 0.0f,s[1], u[1], -f[1], 0.0f,s[2], u[2], -f[2], 0.0f,0.0f, 0.0f, 0.0f, 1.0f );示例:模板库 glm 数学库的 LookAt 相关的代码 lookAtRH (右)/ lookAtLH(左)
视图矩阵
① 相机位置姿态矩阵
即:将相机坐标系中点的坐标变换到世界坐标系中。
相机本身的变换(先旋转再平移),有了相机的旋转矩阵R和平移矩阵T,就可以轻易的计算得出相机-世界矩阵:
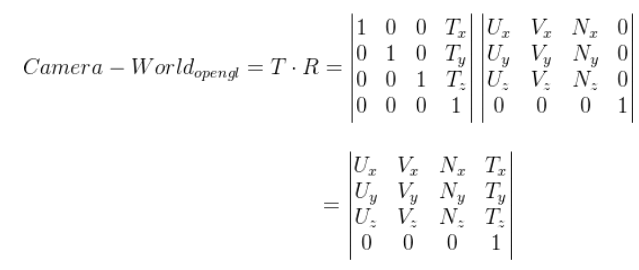
② 视图矩阵/观察矩阵
即:将世界坐标系中点的坐标变换到相机坐标系中。
相机本身变换的逆变换(先平移再旋转)

注1:正交矩阵的一个重要性质就是逆等于转置;
注2:位移矩阵的逆矩阵就是反向位移矩阵;
投影矩阵
① 透视投影矩阵


透视投影矩阵推导过程:https://zhuanlan.zhihu.com/p/104039832
右手系(如:OpenGL)的标准透视投影矩阵形式(矩阵左乘形式):
注:标准视景体Z的范围 [-1, 1](即将 映射到
)

矩阵右乘形式 :

左手系(如:DirectX)的透视投影矩阵形式(矩阵右乘形式)
注:标准视景体Z的范围 [0, 1]

② 正交投影矩阵

