【深度学习】#10 注意力机制
主要参考学习资料:
《动手学深度学习》阿斯顿·张 等 著
【动手学深度学习 PyTorch版】哔哩哔哩@跟李牧学AI
目录
- 注意力提示
- 生物学中的注意力提示
- 查询、键和值
- 注意力汇聚
- 注意力评分函数
- 掩蔽softmax操作
- 加性注意力
- 缩放点积注意力
- Bahdanau注意力
- 多头注意力
- 自注意力和位置编码
- 自注意力
- 位置编码
- 1. 绝对位置信息
- 2. 相对位置信息
- Transformer
- 编码器-解码器
- 逐位前馈网络(FFN)
- 层规范化(LR)
概述
- 注意力汇聚结合当前位置的预测任务自主地为不同输入分配权重。
- 输入的权重由相关性决定,计算相关性的函数称为注意力评分函数。
- Bahdanau注意力是注意力机制在Seq2Seq模型中的应用。
- 多头注意力对同一组信息分别做不同的注意力汇聚再组合。
- 自注意力计算同一序列内部任意两个元素的关系。
- Transformer是一种完全基于注意力机制的模型。
注意力提示
生物学中的注意力提示
人类每时每刻会接收大量的感官输入,这些感官输入远远超出了大脑能够完全处理的能力。但是并非所有刺激的影响都是同等的,意识的汇聚和专注使我们能够在复杂的环境中将注意力引向感兴趣的物体。
注意力的焦点受非自主性提示和自主性提示影响。非自主性提示基于环境中物体的突出性和易见性,例如人群中偶然出现身着奇装异服的人会吸引我们的目光;自主性提示受认知和意识的控制,例如我们想在人群中找到自己的朋友,会主动留意具有与朋友相关特征的事物。
查询、键和值
注意力机制是基于自主性提示的。在注意力机制中,自主性提示被称为查询,而感官输入被称为值,键是从感官输入中提取的特征表示,为非自主性提示,键和值是一一对应的。针对当前的预测任务,模型会先给出一个查询,通过将查询与每个键匹配判断每个值与查询的相关性,进而通过注意力汇聚为值赋予不同的权重,最终将值加权得到为当前预测任务提供参考的上下文变量。以论文写作中的文献查找为例,查询就是我们的研究任务,键就是我们在初步判断文献相关性时关注的标题和摘要,而值是文献具体的文章内容。

注意力汇聚
查询和键之间的交互形成了注意力汇聚,注意力汇聚有选择性地汇聚了值以生成最终的输出。Nadaraya-Watson核回归是一种常用的注意力汇聚方法。
一个比较通用的注意力汇聚公式形式如下:
f ( x ) = ∑ i = 1 n α ( x , x i ) y i f(x)=\displaystyle\sum^n_{i=1}\alpha(x,x_i)y_i f(x)=i=1∑nα(x,xi)yi
其中 x x x是查询, ( x i , y i ) (x_i,y_i) (xi,yi)是键值对。 α ( x , x i ) \alpha(x,x_i) α(x,xi)是分配给值 y i y_i yi的注意力权重,通过 x x x和 x i x_i xi的相关性得到。最后使用注意力权重对值进行加权和得到输出。权重是非负的,且总和为 1 1 1。
注意力权重通常使用核函数计算,它是数学中可用于衡量样本相似性的函数。Nadaraya-Watson核回归使用了高斯核,其定义为:
K ( x , x i ) = 1 2 π exp ( − ( x − x i ) 2 2 ) K(x,x_i)=\displaystyle\frac1{\sqrt{2\pi}}\exp\left(-\frac{(x-x_i)^2}2\right) K(x,xi)=2π1exp(−2(x−xi)2)
x x x和 x i x_i xi越相关(距离越近),则该核函数越接近 1 2 π \displaystyle\frac1{\sqrt{2\pi}} 2π1,反之则趋向于 0 0 0。
为了得到注意力权重,我们还需对其进行归一化处理:
α ( x , x i ) = exp ( − 1 2 ( x − x i ) 2 ) ∑ j = 1 n exp ( − 1 2 ( x − x j ) 2 ) = s o f t m a x ( − 1 2 ( x − x i ) 2 ) \alpha(x,x_i)=\displaystyle\frac{\displaystyle\exp\left(-\frac12(x-x_i)^2\right)}{\displaystyle\sum^n_{j=1}\exp\left(-\frac12(x-x_j)^2\right)}=\mathrm{softmax}\left(-\frac12(x-x_i)^2\right) α(x,xi)=j=1∑nexp(−21(x−xj)2)exp(−21(x−xi)2)=softmax(−21(x−xi)2)
最后我们得到基于Nadaraya-Waston核回归的注意力汇聚模型为:
f ( x ) = ∑ i = 1 n s o f t m a x ( − 1 2 ( x − x i ) 2 ) y i f(x)=\displaystyle\sum^n_{i=1}\mathrm{softmax}\left(-\frac12(x-x_i)^2\right)y_i f(x)=i=1∑nsoftmax(−21(x−xi)2)yi
该非参数的注意力汇聚模型需要大量数据才能收敛到最优结果,通过将查询 x x x和键 x i x_i xi之间的距离乘以可学习参数 w w w可以提升其泛化能力:
f ( x ) = ∑ i = 1 n s o f t m a x ( − 1 2 ( ( x − x i ) w ) 2 ) y i f(x)=\displaystyle\sum^n_{i=1}\mathrm{softmax}\left(-\frac12((x-x_i)w)^2\right)y_i f(x)=i=1∑nsoftmax(−21((x−xi)w)2)yi
注意力评分函数
在注意力汇聚模型中,最核心的组件是其softmax操作中的部分,被称为注意力评分函数,简称评分函数。评分函数是未经标准化的注意力权重,决定了模型如何聚焦于输入的不同部分,其设计直接影响模型的性能。

用数学语言描述,假设有一个查询 q ∈ R q \mathbf q\in\mathbb R^q q∈Rq和 m m m个键值对 ( k 1 , v 1 ) , ⋯ ( k m , v m ) (\mathbf k_1,\mathbf v_1),\cdots(\mathbf k_m,\mathbf v_m) (k1,v1),⋯(km,vm),其中 k ∈ R k \mathbf k\in\mathbb R^k k∈Rk, v ∈ R v \mathbf v\in\mathbb R^v v∈Rv。则注意力函数 f f f为值的加权和:
f ( q , ( k 1 , v 1 ) , … , ( k m , v m ) ) = ∑ i = 1 m α ( q , k i ) v i ∈ R v \displaystyle f(\mathbf{q}, (\mathbf{k}_1, \mathbf{v}_1), \ldots, (\mathbf{k}_m, \mathbf{v}_m)) = \sum_{i=1}^m \alpha(\mathbf{q}, \mathbf{k}_i) \mathbf{v}_i \in \mathbb{R}^v f(q,(k1,v1),…,(km,vm))=i=1∑mα(q,ki)vi∈Rv
其中权重由注意力评分函数 a a a经过softmax运算得到:
α ( q , k i ) = s o f t m a x ( a ( q , k i ) ) ∈ R \alpha(\mathbf{q}, \mathbf{k}_i) = \mathrm{softmax}(a(\mathbf{q}, \mathbf{k}_i))\in \mathbb{R} α(q,ki)=softmax(a(q,ki))∈R
掩蔽softmax操作
在某些情况下,并非所有的值都应该被纳入注意力汇聚中,例如为了进行小批量处理而将序列填充至等长的无意义词元。可以通过指定一个有效序列长度,在计算softmax时过滤掉超出指定范围的位置,称为掩蔽softmax操作。
加性注意力
加性注意力适用于查询和键的向量长度不一致的情况。给定查询 q ∈ R q \mathbf q\in\mathbb R^q q∈Rq和键 k ∈ R k \mathbf k\in\mathbb R^k k∈Rk,加性注意力的评分函数为:
a ( q , k ) = w v ⊤ tanh ( W q q + W k k ) ∈ R a(\mathbf q, \mathbf k) = \mathbf w_v^\top \text{tanh}(\mathbf W_q\mathbf q + \mathbf W_k \mathbf k) \in \mathbb{R} a(q,k)=wv⊤tanh(Wqq+Wkk)∈R
式中可学习的参数为 W q ∈ R h × q \mathbf W_q\in\mathbb R^{h\times q} Wq∈Rh×q、 W k ∈ R h × k \mathbf W_k\in\mathbb R^{h\times k} Wk∈Rh×k和 w v ∈ R h \mathbf w_v\in\mathbb R^h wv∈Rh。该函数将查询和键连接后送入激活函数为tanh的隐藏层得到一个长度为 h h h的向量后与 w v \mathbf w_v wv点积,超参数 h h h为隐藏单元数。
缩放点积注意力
在查询和键具有相同的长度 d d d时,点积可以得到计算效率更高的评分函数。假设查询和键的所有元素都是满足零均值和单位方差的独立的随机变量,则查询和键的点积的均值为 0 0 0,方差为 d d d。为确保点积的方差与向量无关,始终为 1 1 1,我们将点积除以 d \sqrt d d得到缩放点积注意力:
a ( q , k ) = q ⊤ k / d a(\mathbf q, \mathbf k) = \mathbf{q}^\top \mathbf{k} /\sqrt{d} a(q,k)=q⊤k/d
Bahdanau注意力
在上一章的机器翻译问题中,编码器将长度可变的序列转换为固定形状的上下文向量,而解码器根据上一个时间步输出的词元和上下文向量生成新输出的词元,每个词元的预测都使用相同的上下文向量。这种方法的缺点是无法处理较长的句子和捕获复杂的依赖关系。而且在翻译中,生成的词元往往和原句的词元存在一定的对应关系,每一步预测关注的输入词元是不一样的。
Bahdanau等人通过将上下文变量视为注意力汇聚的输出,实现了没有严格对齐限制的可微注意力模型。该模型基于上一章的Seq2Seq模型,只是上下文变量由固定不变的 c \mathbf c c变为每个解码时间步 t ′ t' t′都不一样的 c t ′ \mathbf c_{t'} ct′,它是注意力汇聚的输出:
c t ′ = ∑ t = 1 T α ( s t ′ − 1 , h t ) h t \displaystyle\mathbf{c}_{t'} = \sum_{t=1}^T \alpha(\mathbf{s}_{t' - 1}, \mathbf{h}_t) \mathbf{h}_t ct′=t=1∑Tα(st′−1,ht)ht
其中,查询是时间步 t ′ − 1 t'-1 t′−1的解码器隐状态 s t ′ − 1 \mathbf s_{t'-1} st′−1,键和值均为编码器隐状态 h t \mathbf h_t ht,注意力权重使用加性注意力计算。
使用注意力机制的编码器-解码器架构如下图所示(嵌入层对词元的独热向量表示作进一步处理,将在第十四章讨论):

多头注意力
在实践中,当给定相同的查询、键和值的集合时,我们希望模型可以基于相同的注意力机制学习不同的行为,然后将不同的行为作为知识组合起来,捕获序列内各种范围的依赖关系。为此,与其只使用一个注意力汇聚,我们可以将查询、键和值通过不同的线性映射得到 h h h组不同的集合,分别送入不同的注意力汇聚中,最后将它们的输出连接在一起,并再通过一个全连接层变换生成最终的输出:

这种设计被称为多头注意力,每个注意力汇聚被称为一个头。给定查询 q ∈ R d q \mathbf q\in\mathbb R^{d_q} q∈Rdq、键 k ∈ R d k \mathbf k\in\mathbb R^{d_k} k∈Rdk和值 v ∈ R d v \mathbf v\in\mathbb R^{d_v} v∈Rdv,每个注意力头 h i ( i = 1 , ⋯ , h ) \mathbf h_i(i=1,\cdots,h) hi(i=1,⋯,h)的计算方法为:
h i = f ( W i ( q ) q , W i ( k ) k , W i ( v ) v ) ∈ R p v \mathbf{h}_i = f(\mathbf W_i^{(q)}\mathbf q, \mathbf W_i^{(k)}\mathbf k,\mathbf W_i^{(v)}\mathbf v) \in \mathbb R^{p_v} hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv
其中可学习的参数包括全连接层的 W i ( q ) ∈ R p q × d q \mathbf W_i^{(q)}\in\mathbb R^{p_q\times d_q} Wi(q)∈Rpq×dq、 W i ( k ) ∈ R p k × d k \mathbf W_i^{(k)}\in\mathbb R^{p_k\times d_k} Wi(k)∈Rpk×dk和 W i ( v ) ∈ R p v × d v \mathbf W_i^{(v)}\in\mathbb R^{p_v\times d_v} Wi(v)∈Rpv×dv,以及注意力汇聚函数 f f f中的参数。带下标的 d d d和 p p p分别是全连接层转换前后的查询、键、值的长度, f f f可以是加性注意力或缩放点积注意力。
将 h h h个头的输出连接起来,并乘以可学习的参数 W o ∈ R p o × h p v \mathbf W_o\in\mathbb R^{p_o\times h p_v} Wo∈Rpo×hpv,我们就得到了多头注意力的最终输出:
W o [ h 1 ⋮ h h ] ∈ R p o \mathbf W_o \begin{bmatrix}\mathbf h_1\\\vdots\\\mathbf h_h\end{bmatrix} \in \mathbb{R}^{p_o} Wo h1⋮hh ∈Rpo
自注意力和位置编码
使用传统注意力机制的Seq2Seq模型仍存在以下问题:
- 每个时间步的计算都依赖前一个时间步的输出,无法并行化处理,只能逐个时间步地串行计算。
- 当序列较长的时候,容易出现梯度消失和梯度爆炸的问题。
因此进一步改进的方向是让模型不使用序列框架,但仍能有处理序列数据的能力,并且避免过长的链式求导过程。达成这个目标的最后一块拼图便是自注意力。
自注意力
自注意力和传统注意力相比,不计算序列之间的交互,而是计算同一序列内部的交互,直接捕捉序列中任意两个元素的关系,不像CNN和RNN一样受局部性限制。

在自注意力中,查询、键和值均为输入序列每一个时间步的输入。给定一个由词元组成的输入序列 x 1 , ⋯ , x n \mathbf{x}_1, \cdots, \mathbf{x}_n x1,⋯,xn,其中任意 x i ∈ R d ( 1 ⩽ i ⩽ n ) \mathbf x_i\in\mathbb R^d(1\leqslant i\leqslant n) xi∈Rd(1⩽i⩽n),该序列的自注意力输出为一个长度相同的序列 y 1 , ⋯ , y n \mathbf{y}_1, \cdots, \mathbf{y}_n y1,⋯,yn,其中:
y i = f ( x i , ( x 1 , x 1 ) , ⋯ , ( x n , x n ) ) ∈ R d \mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \cdots, (\mathbf{x}_n, \mathbf{x}_n)) \in \mathbb{R}^d yi=f(xi,(x1,x1),⋯,(xn,xn))∈Rd
上式中,键值对是每一个时间步的输入,时间步 i i i的输出 y i \mathbf y_i yi的查询为 x i \mathbf x_i xi。自注意力计算时间步 i i i的输入 x i \mathbf x_i xi与序列中所有时间步的输入的相关性,并对所有时间步的输入加权后经注意力汇聚 f f f处理得到输出 y i \mathbf y_i yi。
通过与CNN和RNN的比较可以理解自注意力的优势:

为了更加直观,对于CNN,我们将输入和卷积核均展成一维。对于长度为 n n n的序列和通道(特征)数均为 d d d的输入输出,三种网络的性能分别如下(CNN卷积核大小为 k k k):
| CNN | RNN | 自注意力 | |
|---|---|---|---|
| 计算复杂度 | O ( k n d 2 ) O(knd^2) O(knd2) | O ( n d 2 ) O(nd^2) O(nd2) | O ( n 2 d ) O(n^2d) O(n2d) |
| 最长路径 | O ( n / k ) O(n/k) O(n/k) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) |
| 并行度 | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | O ( n ) O(n) O(n) |
其中最长路径指输入序列中的一个输入能够传递给另一个输入(得到两个输入的相关信息)经过的计算链条长度,并行度指最多可以并行计算的数据量。
可见,CNN和自注意力都具有并行计算的优势,且自注意力的最长路径最短。但自注意力的计算复杂度是序列长度的平方,因此对很长的序列计算效率较低。
位置编码
CNN和RNN均通过更复杂模型的机制利用了序列输入的位置信息,而自注意力只是一次性接收所有输入对它们全部加权,替换输入的位置顺序不会对输入有影响。为了在不让模型更加复杂的限制下使用序列的位置信息,我们向输入表示中添加位置编码来注入相对或绝对的位置信息,而模型需要通过训练学习到输入表示中的位置信息。
简单地添加表示序号的整数会带来一些问题,主要在于编号缺少限制,对于长文本而言,过大的数字会导致模型在学习词义时受到干扰,或产生数值爆炸,文本的长短不一也会给模型的泛化带来困难。
一个有效的位置编码应该在保证每个输入有唯一表示的同时可以无限延伸而不会爆炸,而傅里叶变换的正余弦组合表示正好符合条件,因为三角函数的周期 2 π 2\pi 2π为无理数,所有有理数的三角函数严格唯一。假设输入表示 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d包含一个序列中 n n n个词元的 d d d维表示,位置编码则使用相同形状的位置嵌入矩阵 P ∈ R n × d \mathbf{P} \in \mathbb{R}^{n \times d} P∈Rn×d与之相加(或连接),矩阵第 i i i行、第 2 j 2j 2j列和第 2 j + 1 2j+1 2j+1列上的元素分别为:
p i , 2 j = sin ( i 1000 0 2 j / d ) \displaystyle p_{i, 2j} = \sin\left(\frac{i}{10000^{2j/d}}\right) pi,2j=sin(100002j/di)
p i , 2 j + 1 = cos ( i 1000 0 2 j / d ) \displaystyle p_{i, 2j+1} = \cos\left(\frac{i}{10000^{2j/d}}\right) pi,2j+1=cos(100002j/di)
1. 绝对位置信息
通过线图和热力图我们可以对矩阵在不同行(位置)和不同列(特征)的值进行可视化:

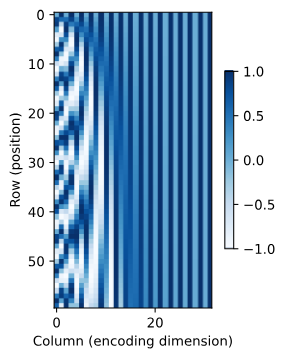
从图中可以看出,输入序列中不同特征的位置编码会随着位置的变化以不同频率波动,多维频率和三角函数的无理数性质共同保证了位置编码的唯一性。同时,低频的特征变化缓慢,便于捕捉长距离关系;高频的特征变化剧烈,便于捕捉细粒度位置。
2. 相对位置信息
该位置编码还能让模型学习到输入序列中的相对位置信息,因为对于一定的偏移量,偏移后位置表示可以转换为对原位置编码的线性组合:
[ p i + δ , 2 j p i + δ , 2 j + 1 ] = [ sin ( ( i + δ ) ω j ) cos ( ( i + δ ) ω j ) ] = [ cos ( δ ω j ) sin ( i ω j ) + sin ( δ ω j ) cos ( i ω j ) − sin ( δ ω j ) sin ( i ω j ) + cos ( δ ω j ) cos ( i ω j ) ] = [ cos ( δ ω j ) sin ( δ ω j ) − sin ( δ ω j ) cos ( δ ω j ) ] [ p i , 2 j p i , 2 j + 1 ] \begin{split}\begin{aligned} &\begin{bmatrix} p_{i+\delta, 2j} \\ p_{i+\delta, 2j+1} \\ \end{bmatrix}\\ =&\begin{bmatrix} \sin\left((i+\delta) \omega_j\right) \\ \cos\left((i+\delta) \omega_j\right) \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\ -\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j) \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) & \sin(\delta \omega_j) \\ -\sin(\delta \omega_j) & \cos(\delta \omega_j) \\ \end{bmatrix} \begin{bmatrix} p_{i, 2j} \\ p_{i, 2j+1} \\ \end{bmatrix}\\ \end{aligned}\end{split} ===[pi+δ,2jpi+δ,2j+1][sin((i+δ)ωj)cos((i+δ)ωj)][cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)][cos(δωj)−sin(δωj)sin(δωj)cos(δωj)][pi,2jpi,2j+1]
Transformer
自注意力的并行计算和最短最长路径使其在设计深度网络架构上具有很大的优势。Transformer模型采用编码器-解码器架构,但是和使用注意力的Seq2Seq不同,它是一种完全基于注意力机制的模型。

编码器-解码器
Transformer的编码器和解码器分别接收源(输入)序列和目标(输出)序列的嵌入表示与位置编码的和作为输入。
编码器由多个相同的层叠加而成,每个层都有多头自注意力汇聚和逐位前馈网络两个子层。受残差网络启发,每个子层都采用了残差连接,紧接着应用层规范化。残差连接要求对于输入序列对应的每个位置 x ∈ R d \mathbf x\in\mathbb R^d x∈Rd,Transformer编码器都将输出一个 d d d维表示向量。
解码器也由多个相同的层叠加而成,其在编码器中两个子层的基础上插入了第三个子层,称为编码器-解码器注意力层。在编码器-解码器注意力层中,查询来自前一个解码器层的输出,而键和值来自整个编码器的输出。而在处理来自目标序列的输入时,解码器的多头自注意力只能考虑当前位置之前的所有位置,即计算 x i \mathbf x_i xi的输出 y i \mathbf y_i yi时,假装当前序列长度为 i i i,以确保当前的预测仅依赖已生成的输出词元,因此采取了掩蔽注意力。
逐位前馈网络(FFN)
在Transformer中,注意力一次性接收一整个序列而不是序列中每个时间步的词元作为输入,一个长度为 n n n、特征数为 d d d的序列样本的输入维度是 n × d n\times d n×d,然而序列长度 n n n是可变的,这让输入维度固定的全连接层无法直接处理一个样本。但是在批量化处理中,同一个全连接层可以处理不同批量大小 b b b的批量样本。
对于形状为 ( b , n , d ) (b,n,d) (b,n,d)一个批量的序列样本,我们可以将其变换成 ( b × n , d ) (b\times n,d) (b×n,d),把序列长度 n n n合并到批量大小 b b b中,则输入维度固定为 d d d。这相当于把序列拆散为词元,将词元视为一个样本处理。在全连接层处理过后,我们仍将其形状还原为 ( b , n , d ) (b,n,d) (b,n,d)。由于该网络逐个位置地处理词元,而不是直接处理整个序列,因此被称为逐位前馈网络。
层规范化(LR)
在之前介绍的批量规范化中,我们从特征维度上对一个批量的所有样本进行规范化,然而该方法无法处理可变序列输入。在逐位前馈网络中提到,直接对序列做批量化处理要求所有序列的长度一致,如果通过填充词元来实现这一点,则填充词元将扰乱批量规范化对其他词元的均值和方差的统计,影响模型收敛。同时,填充词元也会占用显存,产生更多的无效计算,尤其是自然语言处理的样本分布往往是少数序列极长,多数较短,将会有大量的序列被填充大量填充词元。
层规范化则从样本维度上独立地对每个样本的所有特征进行归一化,在无视批量的同时还保留了特征间关系,在序列处理模型中替代了批量规范化的地位。
总结一下,在Transformer中,源序列和目标序列经嵌入表示和位置编码相加分别作为编码器和解码器的输入。在编码器中,源序列的输入经多次自注意力汇聚、逐位前馈网络处理得到原始的上下文变量。在解码器的每个相同的层中,掩蔽注意力仅接收当前预测位置之前的目标序列,并将上一个位置的预测结果作为查询对来自编码器的原始上下文变量进行注意力汇聚操作,其输出送入逐位前馈网络。每个子层之间都采取了残差连接和层规范化处理。
