当前位置：首页 > news >正文

MATLAB 控制系统设计与仿真 - 38

news 来源：原创 2025/4/20 9:25:57

多变量系统 $H_{\infty}$ 控制器设计实例1

考虑如下给出的多变量系统模型：

$G(s)=\begin{bmatrix} \frac{0.806s+0.264}{s^2+1.15s+0.202} &\frac{-15s-1.42}{s^3+12.8s^2+13.6s+2.36} \\ \frac{1.95s^2+2.12s+0.49}{s^3+9.15s^2+9.39s+1.62}&\frac{7.15s^2+25.8s+9.35}{s^4+20.8s^3+116.4s^2+111.6s+18.8} \end{bmatrix}$

考虑混合灵敏度问题，引入加权矩阵：

$W_1(s)=\begin{bmatrix} \frac{100}{s+0.5} & 0\\ 0 & \frac{100}{s+1} \end{bmatrix} \\ W_2=\begin{bmatrix} 10^{-5} & 0\\ 0 & 10^{-5} \end{bmatrix} \\ W_3(s)=\begin{bmatrix} \frac{s}{100} & 0\\ 0 & \frac{s}{200} \end{bmatrix}$

设计 $H_{\infty}$ 鲁棒控制器，并绘制闭环系统的阶跃响应曲线及开环系统的奇异值曲线。

MATLAB代码如下：

clear all;clc;
s=tf('s');
g11=tf([0.806 0.264],[1 1.15 0.202]);
g12=tf([-15 -1.42],[1 12.8 13.6 2.36]);
g21=tf([1.95 2.12 0.49],[1 9.15 9.39 1.62]);
g22=tf([7.15 25.8 9.35],[1 20.8 116.4 111.6 18.8]);
G=[g11 g12; g21 g22];
W1=[100/(s+0.5) 0; 0 100/(s+1)];
W2=tf(1)*[10^-5 0; 0 10^-5];
W3=[s/100 0;0 s/200];
P=augtf(G,W1,W2,W3);
[K,CL,gamma]=hinfsyn(P);
figure(1)
step(feedback(G*K,eye(2)),0.1);
grid on;
figure(2)
sigma(G*K)
grid on;

程序运行结果如下：

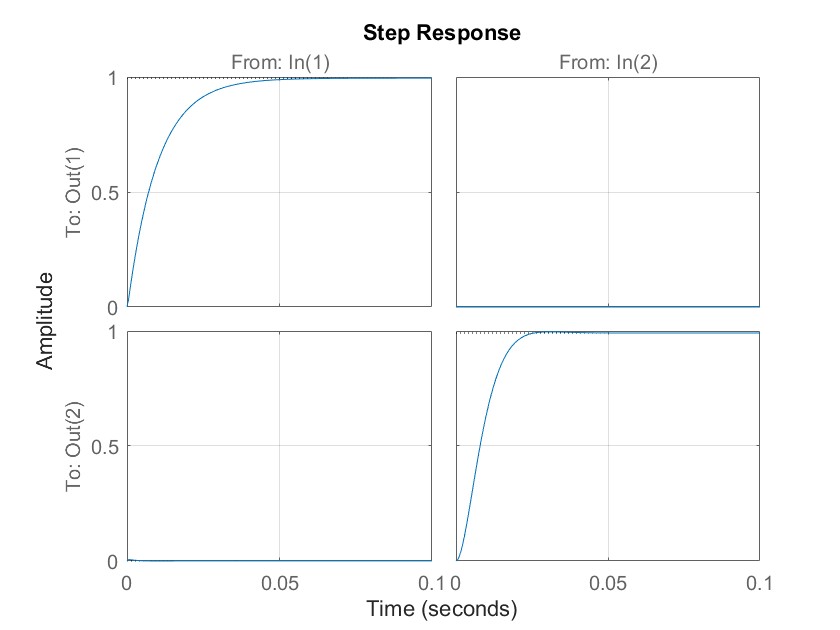
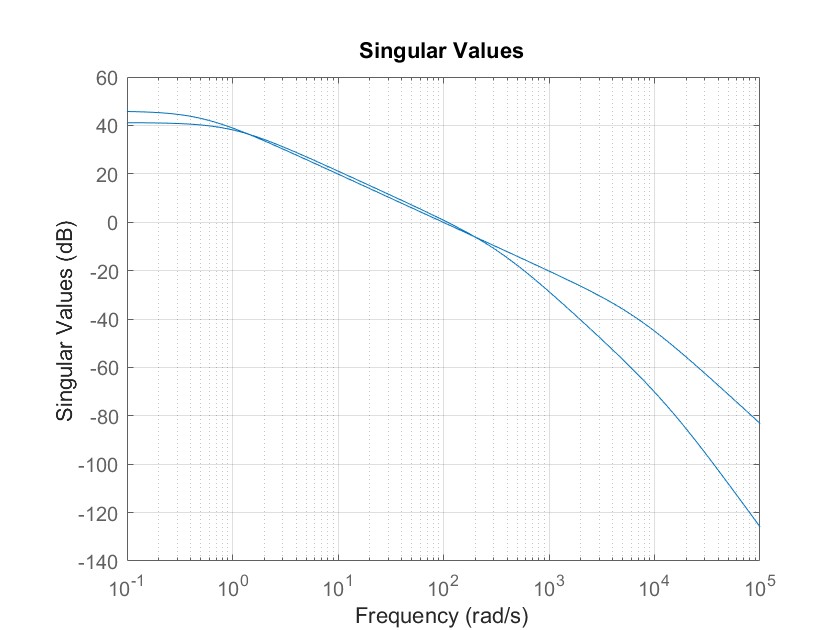
从结果可以看出，得出的阶跃响应是很理想的，第1路阶跃输入作用于子系统时能得出很好的y1输出，而y2几乎为0.当第2路输入单独作用时效果也很好，然而这样设计出来的控制器阶次是相当高的。例如K(1,2)控制器的传递函数为：

>> tf(K(1,2))ans =9624 s^13 + 2.982e08 s^12 + 1.562e12 s^11 + 4.93e13 s^10 + 5.738e14 s^9 + 3.033e15 s^8 + 7.55e15 s^7 + 1.013e16 s^6 + 7.884e15 s^5 + 3.663e15 s^4 + 1.014e15 s^3 + 1.618e14 s^2 + 1.355e13 s + 4.52e11  --------------------------------------------------------------------------------------------------------------------s^14 + 2.089e04 s^13 + 1.005e08 s^12 + 3.42e10 s^11 + 8.161e11 s^10 + 6.824e12 s^9 + 2.461e13 s^8 + 4.801e13 s^7  + 5.644e13 s^6 + 4.205e13 s^5 + 2.019e13 s^4 + 6.189e12 s^3 + 1.165e12 s^2 + 1.223e11 s + 5.466e09Continuous-time transfer function.
Model Properties

另外根据阶跃响应结果可知，y22的响应速度和y11相比显得很慢，因此需要加重y22的权重。

令：

$W1=\begin{bmatrix} \frac{100} {(s+0.5)} & 0 \\ 0& \frac{1000}{s+1} \end{bmatrix}$

重新设计最优 $H_{\infty}$ 鲁棒控制器，MATLAB代码为：

W1=[100/(s+0.5) 0; 0 1000/(s+1)];
P=augtf(G,W1,W2,W3);
[K,CL,gamma]=hinfsyn(P);
figure(1)
step(feedback(G*K,eye(2)),0.1);
grid on;
figure(2)
sigma(G*K)
grid on;

程序运行结果为：

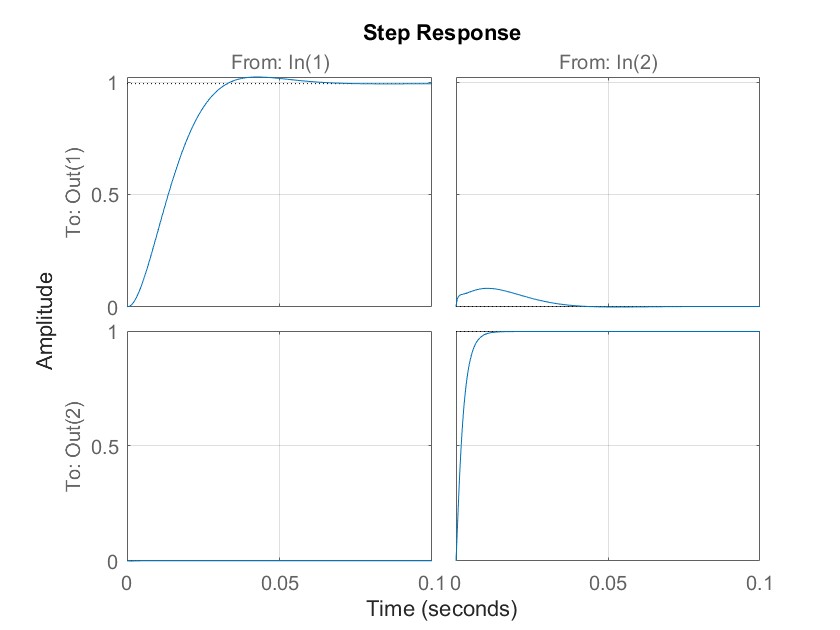
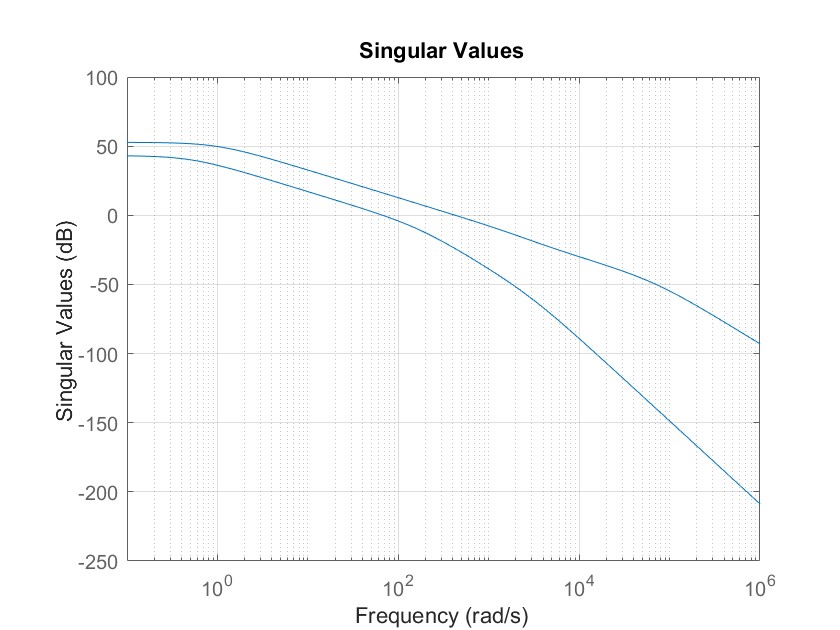
由上图可知，在新的控制器下，y22效果明显改善。

新的控制器传递函数为：

tf(K(1,2))ans =1.07e07 s^13 + 3.147e10 s^12 + 6.161e12 s^11 + 1.741e14 s^10 + 1.939e15 s^9 + 1.002e16 s^8 + 2.471e16 s^7         + 3.306e16 s^6 + 2.574e16 s^5 + 1.2e16 s^4 + 3.343e15 s^3 + 5.393e14 s^2 + 4.591e13 s + 1.571e12------------------------------------------------------------------------------------------------------------------s^14 + 7.391e04 s^13 + 1.707e08 s^12 + 3.072e10 s^11 + 6.998e11 s^10 + 5.765e12 s^9 + 2.068e13 s^8 + 4.025e13 s^7 + 4.725e13 s^6 + 3.517e13 s^5 + 1.688e13 s^4 + 5.172e12 s^3 + 9.735e11 s^2 + 1.022e11 s + 4.565e09Continuous-time transfer function.
Model Properties

由于控制器的阶次较高，在实际应用中难以实现，因此可以考虑采用降阶算法降低控制器的阶次。可以采用闭环系统的控制器模型降阶的概念，降低控制器的阶次直接实现降阶。

最后，欢迎大家有问题给我留言。

非常感谢小伙伴们的-点赞-收藏-加关注。