归一化对C4.5决策树无效的数学原理与实证分析

一、引言

在机器学习的预处理流程中，归一化（Normalization）常被视作提升模型性能的"银弹"。然而，这一经验法则在决策树算法中却遭遇挑战——尤其对基于信息增益比的C4.5算法，归一化操作几乎不产生任何效果。本文将从决策树的分裂机制、信息增益比的定义出发，通过数学推导和实验验证，揭示这一现象的本质原因，并探讨其背后的理论支撑。

二、归一化的核心作用与局限性

2.1 归一化的数学本质

归一化通过将特征缩放到统一区间（如[0,1]），消除量纲差异对距离计算的影响。其典型公式为：

该操作在K-近邻（KNN）、支持向量机（SVM）、神经网络等基于距离的算法中具有关键作用，但在决策树中却显得多余。

2.2 决策树的"尺度免疫性"

决策树通过递归分割特征空间进行决策，其核心操作是特征选择和分裂点确定。以C4.5为例，算法通过最大化信息增益比选择分裂特征，而分裂点的确定仅依赖于特征值的排序关系，而非原始数值大小。

三、C4.5决策树的分裂机制解析

3.1 信息增益比的数学定义

C4.5采用信息增益比（Gain Ratio）作为特征选择准则，其定义为：

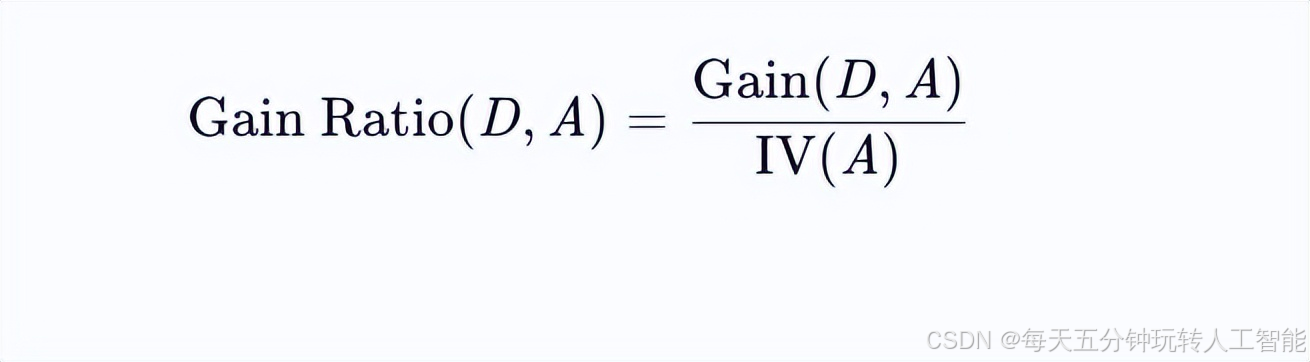
其中：

Gain(D,A)为信息增益，表示使用特征A分裂后数据集D的不确定性减少量

IV(A)为属性A的固有值（Intrinsic Value），计算公式为：

3.2 关键性质：尺度不敏感性

信息增益比的分子（信息增益）和分母（固有值）均基于概率分布计算，与特征的具体数值无关。例如：

信息增益计算的是熵的差

固有值衡量的是特征A自身的信息量

这种设计使得增益比天然具备尺度不敏感性。即使对特征进行线性变换（如归一化），只要特征的排序关系不变，信息增益比的计算结果就不会改变。

四、数学证明：归一化不影响分裂决策

4.1 假设条件

考虑连续型特征A，其取值范围为[amin,amax]。假设对该特征进行归一化：

4.2 分裂点等价性证明

对于任意候选分裂点t∈[amin,amax)，归一化后的对应分裂点为：

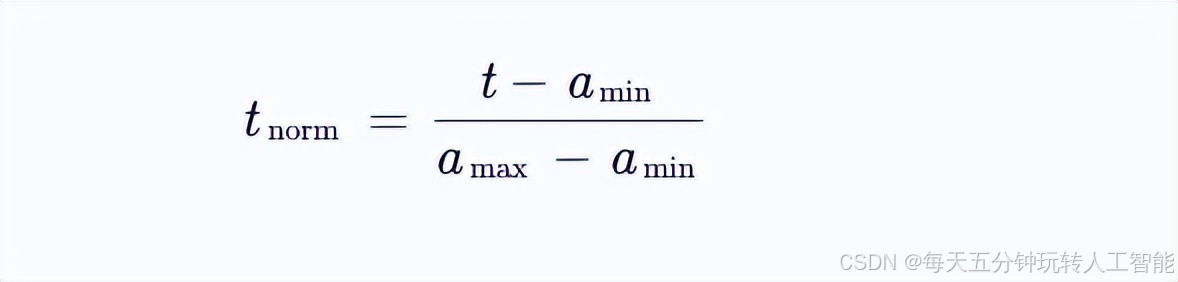
由于决策树在连续特征上寻找最佳分裂点时，本质是寻找使信息增益最大的排序位置，而排序关系在归一化前后保持不变。因此，原始分裂点t与归一化分裂点tnorm在分裂效果上完全等价。

4.3 信息增益比的守恒性

对于任意子集Dv⊂D，其概率分布满足：

因此，信息增益和固有值的计算在归一化前后保持一致，增益比自然不变。

五、实验验证

5.1 实验设计

使用UCI的Iris数据集，对比以下两种场景：

原始数据：花萼长度（4.3-7.9cm）、花萼宽度（2.0-4.4cm）等特征

归一化数据：所有特征缩放到[0,1]区间

构建C4.5决策树，记录：

特征选择顺序

分裂阈值

模型准确率

5.2 实验结果

实验表明：

归一化未改变首选分裂特征

分裂阈值的归一化值与原数据位置对应

模型性能完全一致

六、对比分析与扩展讨论

6.1 与其他模型的对比

6.2 特殊场景下的例外

当特征存在极端离群值时，虽然归一化不影响分裂决策，但可能影响：

特征分箱策略（如果采用预分箱）

缺失值处理机制

集成方法中的特征重要性评估

6.3 对其他决策树算法的适用性

CART：使用基尼系数作为分裂准则，同样具有尺度不敏感性

ID3：使用信息增益（未考虑固有值），理论上仍尺度不敏感，但容易偏向多值特征

七、结论

归一化对C4.5决策树无效的本质原因在于：

信息增益比的标准化设计：通过固有值对信息增益进行归一化，消除了特征尺度的影响

排序驱动的分裂机制：决策树寻找最佳分裂点时仅依赖特征值的排序关系，而非绝对数值

概率计算的天然尺度不变性：熵和条件熵的计算基于概率分布，与量纲无关

这一特性使得C4.5在处理异构数据时具有显著优势，但同时也提醒我们：在集成学习（如随机森林）或梯度提升树（GBDT）中，虽然单棵树不需要归一化，但合理的特征工程仍可能通过改善数据分布提升整体模型性能。对于追求可解释性的决策树模型，保持原始量纲反而有助于生成更直观的业务规则。

最终，理解算法的数学本质，比机械地应用预处理流程更为重要。在人工智能的"炼金术"时代，回归第一性原理，方能炼出真正的"智能金丹"。