当前位置：首页 > news >正文

递归、搜索和回溯算法《递归》

news 来源：原创 2025/4/29 7:00:12

在之前的优选算法当中我们已经学习了一些基本的算法，那么接下来我们就要来学习算法当中的一大重要章节——递归、搜索和回溯算法，其实也就是大家常常听到的dfs、bfs；其实本质就是递归，在学习搜索、回溯等算法的过程当中我们会先来了解算法的一些名词，之后再通过算法题来明白算法具体是如何使用的，最后在通过几道练习题来巩固算法。在算法题的讲解当中还是通过题目解析、算法原理讲解、代码实现三步来带你完全理解对应的算法题。在本篇当中我们就来复习之前在C语言当中就学习到的递归，并且本次学习递归会和之前初次学习的角度不同，相信通过本篇的学习会让你不再惧怕递归，一起加油吧！！！

1.递归复习与再理解

通过之前C语言的学习我们就知道递归其实就是函数递归，其本质就是函数自己调用自己。从刚开始学习递归的时候的斐波那契数列再到数据结构当中二叉树当中遍历二叉树、排序当中的快速排序与归并排序都是运用了递归，所以通过之前的学习其实现在我们已经有了基本的递归思维，只不过在之前的学习当中在运用递归的时候通常都要将递归的函数展开图给画出来之后才能理解递归，虽然这样也能理解递归的实现，但是当某个函数递归的展开图很复杂的时候，其实画函数展开图的方式其实反而是阻碍我们理解递归的。

因此接下来再次理解递归就从更加本质的方向去理解，以上我们已经回想起来了递归是什么，那么接下来在此将会通过为什么要使用递归、如何理解递归、如何写好一个递归三个过程来透彻的理解递归。

1.1 为什么要使用递归

首先总结之前使用递归的地方，我们就要思考为什么要使用递归？

在之前二叉树遍历，快速排序等使用递归其实都是一直在解决相同的子问题，此时相比使用迭代递归实现的代码就较为简练，因为每个子问题都是一样的，那么这时候就只需要实现一份代码就可以解决问题。

在遍历二叉树时遍历一棵树可以看作依次向访问二叉树的节点依次再遍历该节点的左子树和右子树，到遍历该节点的左节点和右节点时又可以将其的左子树看作一个要进行遍历的二叉树；执行的操作和与其父节点是相同的，遍历到右节点也如此。在访问二叉树要解决的相同子问题是依次访问二叉树的根节点；左子树；右子树。到了左子树或者右子树当中进行的操作也是和之前是一样的，那么此时就适合使用递归来解决。

再快速排序当中每一步我们要进行的操作就是将给定的数组进行调整，调整之后使得返回的下标左侧的元素值小于返回下标的值；右侧的元素值大于返回下标的值。因此在快速排序当中要解决的相同子问题就是找出对应的基准值将原数组划分为两个部分。之后对子数组进行的操作也相同的，那么此时就可以使用到递归。

在归并排序当中需要解决的相同子问题就是把给定的左子数组形成有序序列，再把右子数组形成有序序列，最后再将左右两个有序序列形成有序序列。在此解决的子问题都是一样的，因此就适合使用递归。

1.2 如何更好的理解递归

通过以上我们就知道了为什么在一些场景当中要使用递归，那么接下来就来讲解如何更好的理解递归。

在之前写二叉树的前序遍历、中序遍历、后序遍历的时候我们都是通过画递归的函数展开图来理解递归具体的实现效果是什么样的。

//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}

以上这样确实能让我们更好的理解，但是问题是如果每实现一个递归都要画递归的展开图也太繁琐了，有没有什么更加简单的方式理解递归呢？

其实是有的，那就是从宏观的角度去看递归，具体的思考方式就是不要再去在意递归的具体展开过程，而是将递归当中一个黑盒，我们不需要知道黑盒当中具体是怎么实现的，我们只需要将对应的数据丢给它，相信它能实现得到我们要的结果，最后把结果得到即可。最后将函数的出口设计好即可。

总的来说宏观的看待递归的过程需要有以下的三点要注意：

1.不要在意递归的细节展开图
2.把递归的函数当作一个黑盒
3.相信这个黑盒一定能完成我们要求的任务

例如以上实现二叉树的中序遍历时，目的其实就是遍历二叉树的根节点、左子树、右子树，那么就只需要先调用对应的中序遍历函数相信它能将左子树的中序遍历结果输出给我们，之后我们只需要把当前节点的数据打印出来即可，之后再先调用对应的中序遍历函数相信它能将右子树的中序遍历结果输出给我们。最后我们再将中序遍历时当前节点值为NULL的情况进行特殊判断。

1.3 如何写好递归

以上我们了解了如何宏观的理解递归，那么接下来我们就要来了解如何在宏观的角度下写好递归的代码

其实我们只需要进行以下的三个操作即可

1.找到相同的子问题（函数头的设计）
2.只关心某个子问题是如何解决的（函数体的书写）
3.注意函数的出口

接下来我们就按照以上的思路来试着实现快速排序和归并排序的伪代码

首先是快速排序当作要解决的相同子问题就是找到对应子数组内的基准值，并且在解决这个子问题的时候需要给函数提供数组起始下标和终止下标以及数组的指针。那么此时递归函数的函数头就需要有三个参数，即数组指针、起始下标、终止下标。解决该子问题就是在对应区间的数组内找到对应的基准值，因此函数体内就需要找出对应数组区间内的基准值元素下标。最后函数的出口就是当对应子数组内起始下标大于等于终止的下标时就返回。

伪代码实现如下所示：

而在归并排序当中要解决的相同子问题就是把对应区间内的数组排序好，并且在解决这个子问题的时候需要给函数提供数组起始下标和终止下标以及数组的指针。那么此时递归函数的函数头就需要有三个参数，即数组指针、起始下标、终止下标。接下来函数体内要实现的就是对对应的子数组进行排序。最后函数的出口就是当左区间的下标大于右区间的下标时。

实现的伪代码如下所示：

1.4 二叉树递归算法题再理解

以上我们从宏观的方向再对递归进行了理解，那么接下来我们就试着对之前在二叉树算法题章节当中写过的算法题再写一遍，这次使用的是宏观的角度来写题。

注：在此就不再进行讲解，算法的链接可以看之前算法题章节

二叉树算法题-CSDN博客

2.递归算法练习题

以上我理解了递归，那么接下来就通过以下的算法题来巩固之前学习大的知识

2.1 汉诺塔

面试题 08.06. 汉诺塔问题 - 力扣（LeetCode）

题目解析

通过以上的题目描述就可以看出该撒算法题压哦我们实现的是将给定的第一个圆盘A当中的所有圆珠移动到圆盘C上，最后圆盘C上圆珠的顺序要和原来圆盘A当中完全一直。也就是将数组A当中的元素移动到数组C当中，最终移动到数组C的元素顺序要和数组A完全一样。

接下来我们就来看看n=1，2，3时具体的圆珠是怎么在三个盘之间移动的

n==1

当n为1时只需要将A当中的盘珠直接移动到C即可

n==2

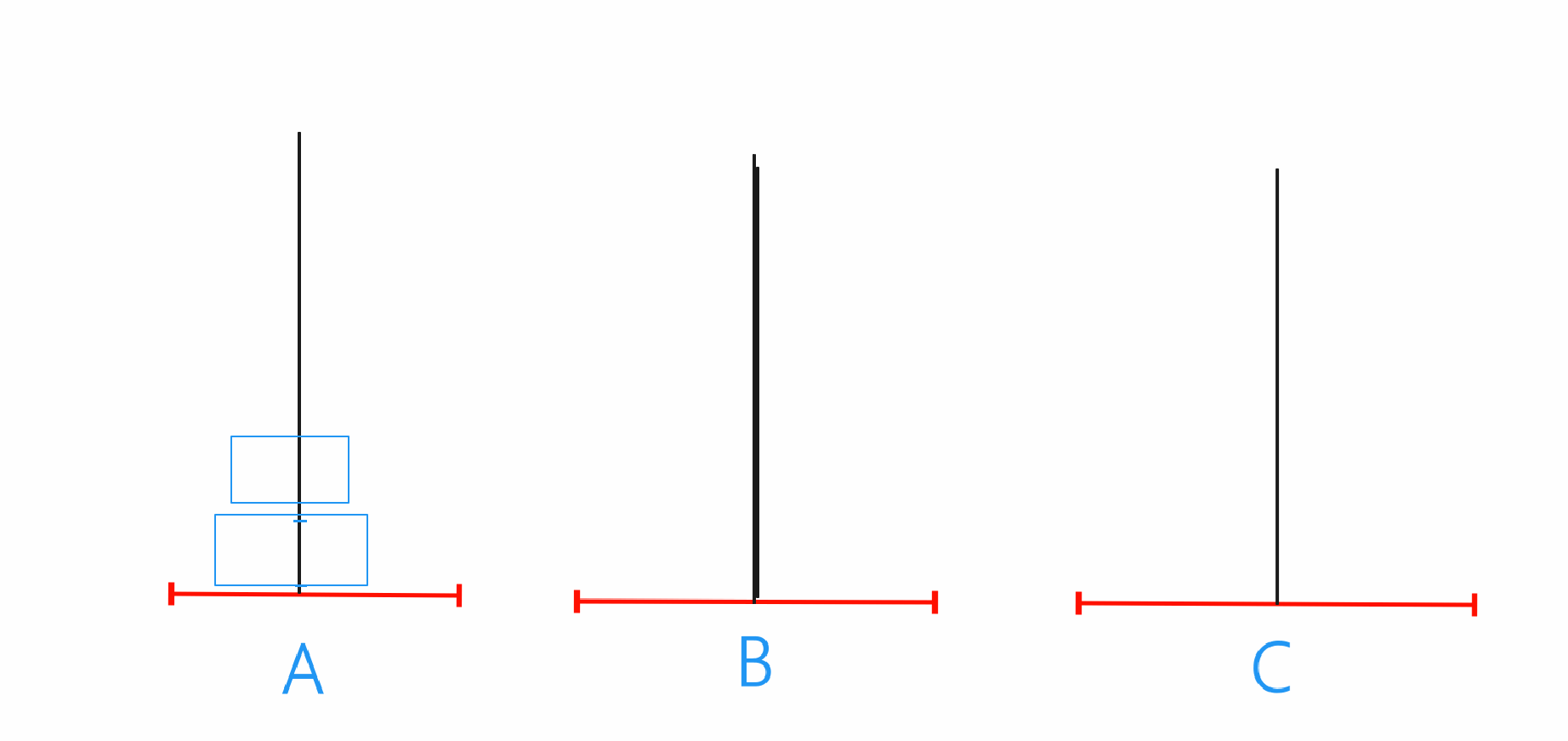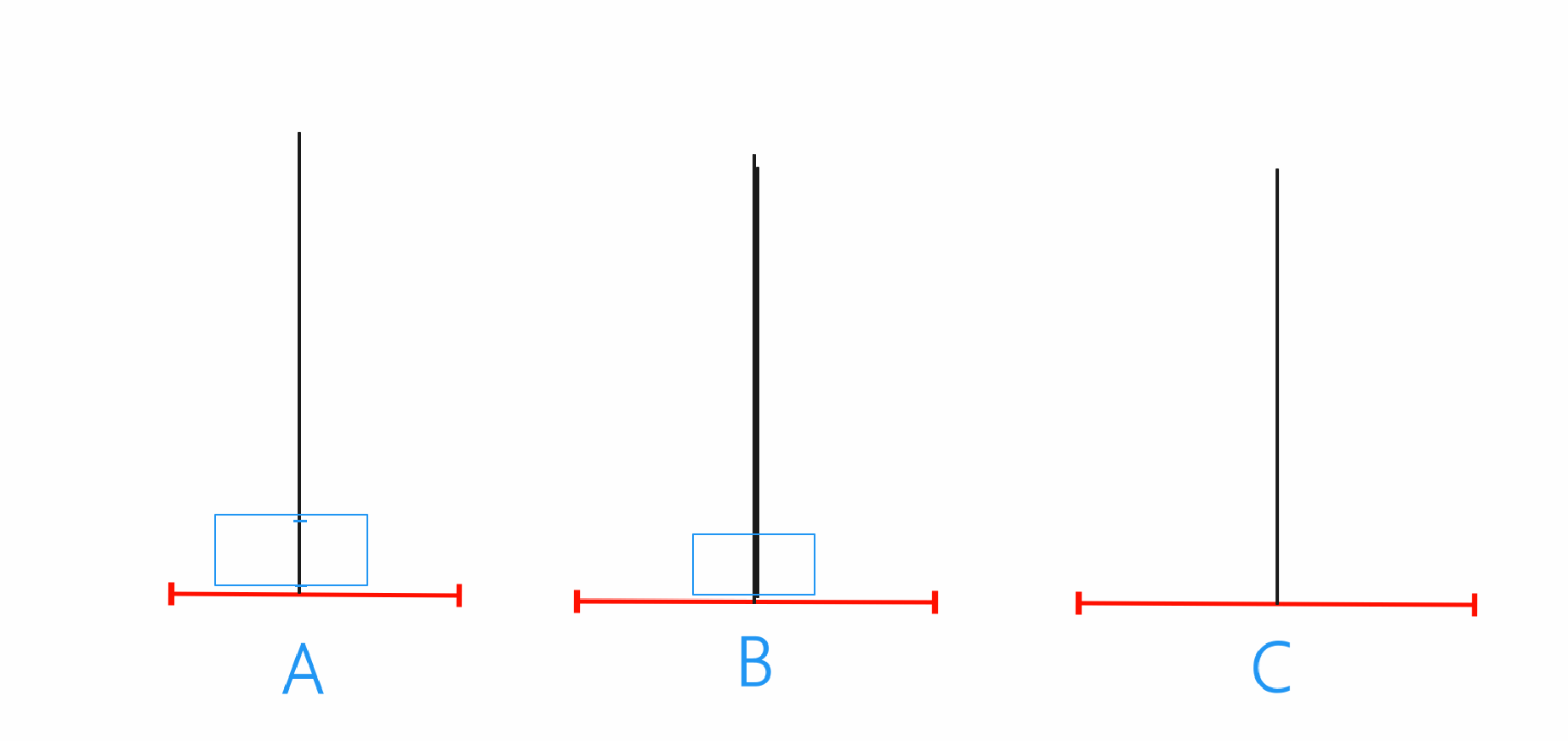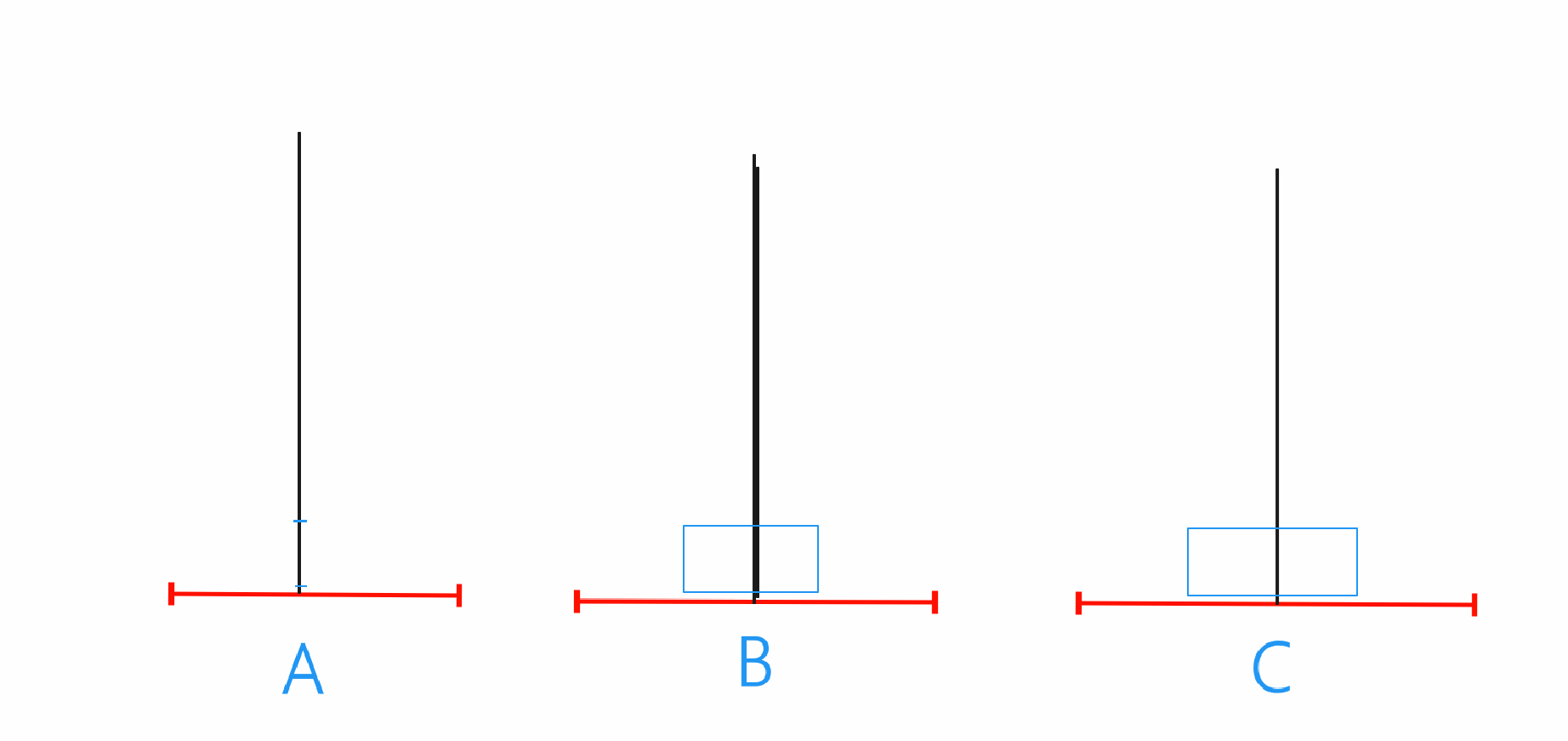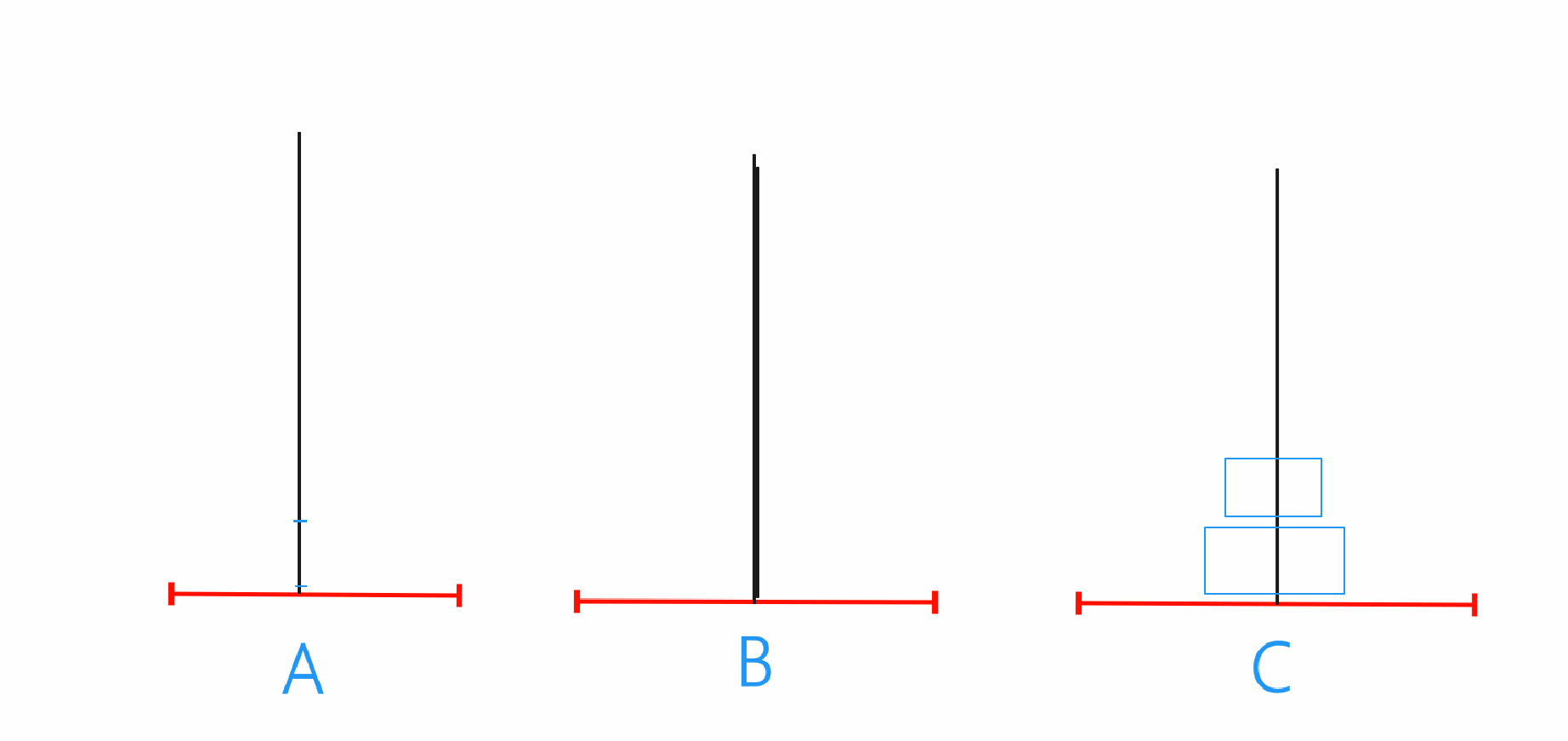
在n为2时就需要先将A当中的最上的那个圆珠移动到B上，之后再将A的最底下爱的圆珠移动到C，最后将B上的圆珠移动到C

n==3

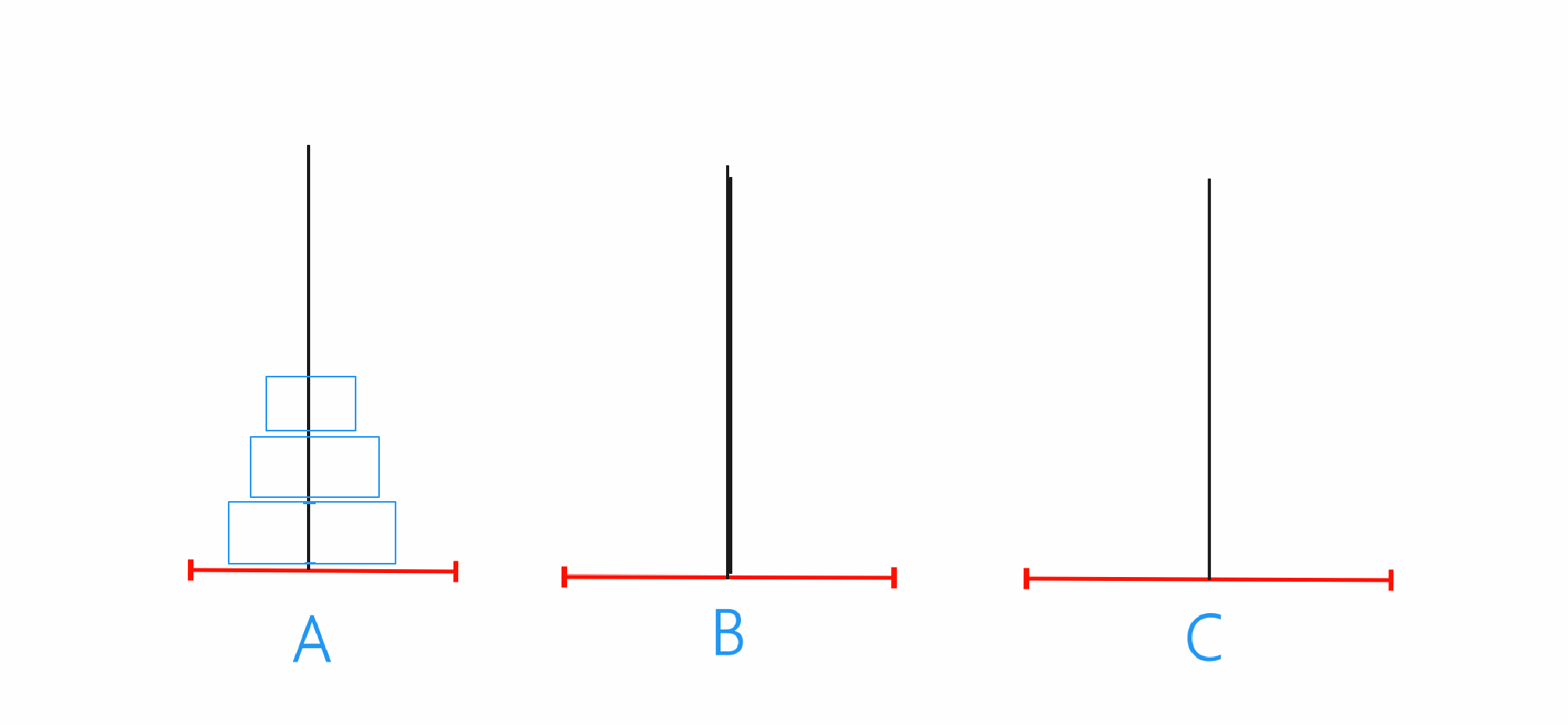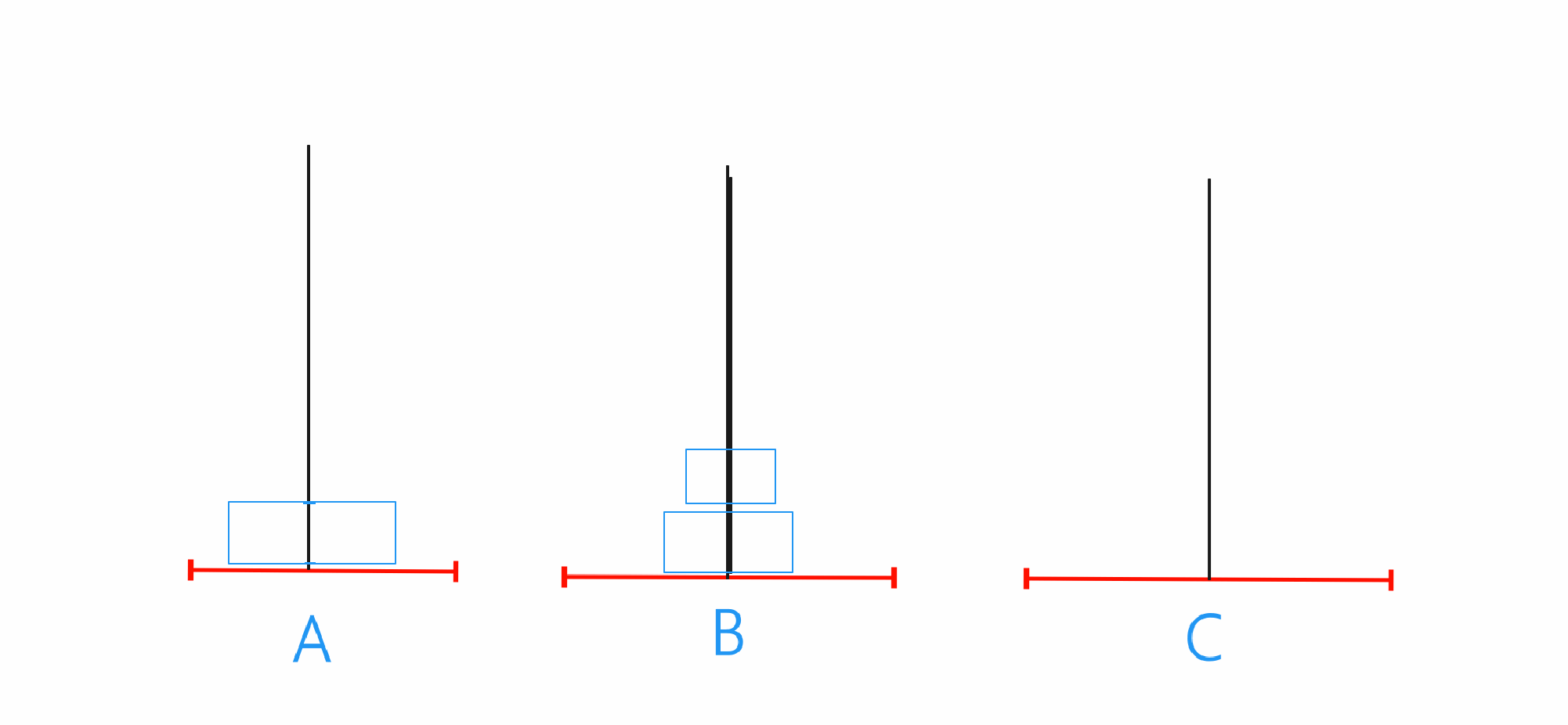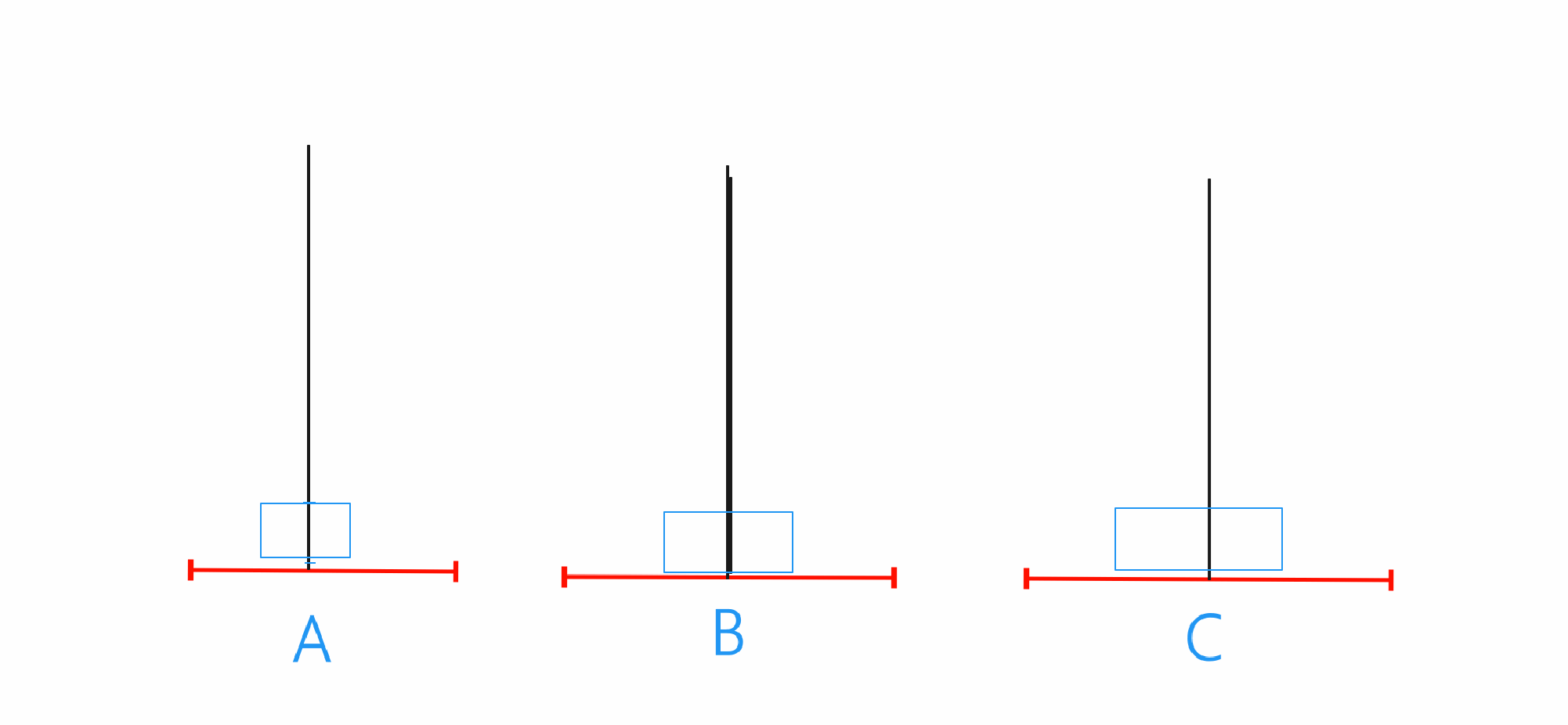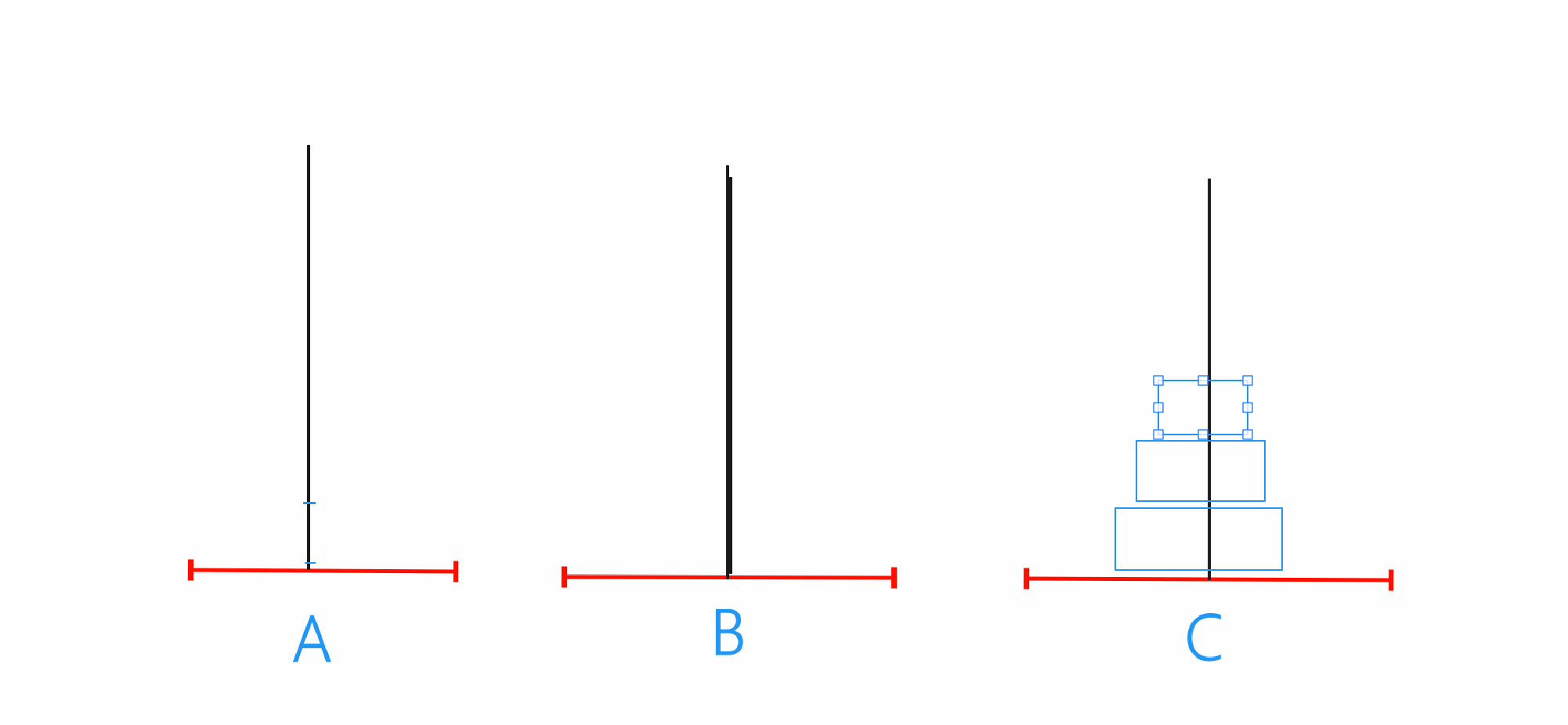
当n==3的时候就只需要先将A当中前两个借助C移动到B，之后再将A的最后一个移动到C，最后将B当中的两个借助A移动到C

算法原理讲解

以上我们就了解该算法题要我们实现的是什么，那么接下来就来试着思考该算法题如何解决

在此通过以上n为1，2，3时候的情况就可以发现解决的过程其实都是通过相识的三步来解决的。第一步是将A当中的前n-1个借助C移动到B，再将A的最后一个移动到C，最后将B的n-1个借助A移动到C

那么在解决每步时候其实就是在解决相同的子问题，而且对于的问题内又是解决步骤相同的子问题，此时就可以使用递归来解决。

接下来就试着来将递归当中的三步分析是什么。

首先是递归当中函数头的设计，此时就要观察重复子问题当中包含哪些。通过以上的步骤图就可以看出在函数当着我们需要知道移动圆珠的个数以及借助的圆盘、目标圆盘。那么就可以得出函数的参数需要4个，分别是移动圆珠的个数、提供圆珠的圆盘、移动中借助的圆盘、目标圆盘。

接下来来分析函数体内该如何实现，也就是只需要观察一个子问题的执行流程，其实就只需要将以上子问题流程图当中的三步执行即可。首先是将n-1个从A借助C移动B，再将A内的最底下的那个移动到C，最后将B中的n-1个借助A移动到C

最后分析函数的出口

当n==1的时候只需要将A当中的最底下的那个移动到C，这就是函数的出口，执行完就从函数返回。

代码实现

以上我们就分析完了汉诺塔这道算法题该如何实现，那么接下来就来试着将以上的算法思路转化为代码

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {//在dfa函数内实现将A的n个圆珠移动到Cdfs(A,B,C,A.size());}//在dfs函数当中A表示提供圆珠的圆盘，B表示借助的圆盘，C表示目标圆盘，n表示圆珠个数void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n){//当n==1时直接将A的最后一个移动到Cif(n==1){   C.push_back(A.back());A.pop_back();return;}//函数有体实现//1：将A当中的n-1个借助C移动到Bdfs(A,C,B,n-1);//2：将A当中的最后一个移动到CC.push_back(A.back());A.pop_back();//3：将B当中的n-1个借助A移动到Cdfs(B,A,C,n-1);}
};

2.2 合并两个有序链表

21. 合并两个有序链表 - 力扣（LeetCode）

题目解析

通过以上的题目描述就可以看出算法题让我们实现的就是将给定的链表进行反转

算法原理讲解

这道题其实在数据结构链表的学习当中我们就已经实解决过了，但是之前我们使用的迭代的方式实现的，而这次我们将从另一角度来解决。

我们先来看以上的示例1
在示例1当中这两个链表就需要从这两个链表的头节点开始，之后对比链表的节点大小之后再小的那个节点的next指针链接到之后剩余的链表的最小值节点当中。

通过以上的步骤图就可以看出其实每一步进行的方式都是一样的，都是找出当中两个链表指针指向的节点当中小的那个节点，之后再该节点的next指针指向剩余的节点的最小值节点。

那么此时我们就发现再该算法题当中存在重复子问题，那么就可以试着使用递归来解决

接下来就试着来将递归当中的三步分析是什么。

首先是递归当中函数头的设计，此时就要观察重复子问题当中包含哪些。通过以上的步骤图就可以看出在函数当着我们需要知道当前两个链表当中指针指向数值小的那个节点。那么就可以得出函数的参数需要2个，分别是另外一个节点的指针，以及数值小的娘那个节点的next指针。函数的返回值就为数值小德那个节点的指针。

接下来来分析函数体内该如何实现，也就是只需要观察一个子问题的执行流程，其实就只需要将以上子问题流程图当中的两步执行即可。首先是将两个链表当中指针指向数值小的那个节点找出，再将该节点的指针的next指针指向剩余节点的返回值。

最后分析函数的出口

当有一个链表为空时就返回另外一个一个链表的节点即可

代码实现

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {//当有一个链表为空时返回if(list1==nullptr)return list2;if(list2==nullptr)return list1;//找出值更小的节点,将值最小的节点的next指针指向剩余节点的返回值if(list1->val<list2->val){list1->next=mergeTwoLists(list1->next,list2);return list1;}else{list2->next=mergeTwoLists(list1,list2->next);return list2;}}
};

2.3 反转链表

206. 反转链表 - 力扣（LeetCode）

题目解析

通过以上的题目描述就可以看出该算法题要我们实现的是将链表进行反转，最后返回反转之后的链表头节点。

算法原理讲解

这道题在之前的链表专题我们也解决过了，只不过在之前的解决这道题时我们是使用创建n1、n2、n3的方式来解决，也就是使用迭代的方式解决的，而这次从不同的角度分析。

首先来看以上的示例1：

通过以上的步骤图就可以看出其实每一步进行的方式都是一样的，都是将当前链表指向的节点之后的节点的next指针指向当前节点，再接收剩余节点的头节点。

那么此时我们就发现再该算法题当中存在重复子问题，那么就可以试着使用递归来解决

接下来就试着来将递归当中的三步分析是什么。

首先是递归当中函数头的设计，此时就要观察重复子问题当中包含哪些。通过以上的步骤图就可以看出在函数当着我们需要知道当前链表的节点。那么就可以得出函数的参数需要1个，是当前节点的指针

接下来来分析函数体内该如何实现，也就是只需要观察一个子问题的执行流程，其实就只需要将以上子问题流程图当中的两步执行即可。首先是将将剩余的节点反转再保存头节点，再将当前节点的之后的节点的next指针指向当前节点，最后将当前节点的next指针值为空

最后分析函数的出口

当链表指针的下一个节点为空时就返回当前的节点

代码实现

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {//当此时当前节点为空时或者的下一个节点为空的时候就返回当前的节点if(head==nullptr || head->next==nullptr)return head;//将剩余的节点进行反转ListNode* ret=reverseList(head->next);//将当前节点的下一个节点的next指针指向当前节点head->next->next= head;//将当前节点的next指针值为空head->next=nullptr;return ret;}
};

注：在本道题当中节点个数可能会出现空，那么此时就需要在函数出口加一条当前节点为空时也返回head，并且要将该条件加到下一个节点为空的判断之前；否则就会出现空指针的解引用。

2.4 两两交换链表中的节点

24. 两两交换链表中的节点 - 力扣（LeetCode）

题目解析

通过以上的题目解析就可以看出该撒算法题要我们实现的是将给定的链表相邻的两个节点位置两两交换，在此我们不能改变节点内的值。

接下来来看示例1：

要将以上的链表相邻节点两两交换，就需要先改变第一个和第二个节点的指针

接下来再继续修改剩余的两个节点指针

算法原理讲解

在通过以上的示例1的分析就发现每次处理的问题都是一样的，都是将当前节点和下一个节点对应的指针进行修改，之后再将当前节点的next指针指向剩余节点。

那么此时该算法题当中解决的就是重复的子问题，在此就可以使用递归来解决，接下来来分析递归当中的三步依次是什么

接下来来分析函数体内该如何实现，也就是只需要观察一个子问题的执行流程，其实就只需要将以上子问题流程图当中的两步执行即可。首先是将将当前节点的下一个节点的next指针指向当前节点，之后再将当前节点的next指针指向剩余的节点，最后返回对应的头节点即可。

最后分析函数的出口

当链表当前节点的指针为空或者的下一个节点为空时就返回当前的节点

代码实现

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {//当前节点为空或者下一个节点为空时就返回当前节点if(head==nullptr || head->next==nullptr)return head;//进行节点next指针的修改，使用ret保存当前头节点的指针ListNode* Next=swapPairs(head->next->next),*ret=head->next;head->next->next=head;head->next=Next;//返回retreturn ret;}
};

2.5 Pow（x, n）- 快速幂

50. Pow(x, n) - 力扣（LeetCode）

题目解析

通过以上的题目描述就可以看出该撒算法题要我们实现的是pow函数，也就是求出指定数的n次幂

算法原理讲解

在这道题当中要实现pow函数，此时我们就要思考应该从什么样的方式去实现，在此如果使用迭代的方式直接将x乘n次，那么按照题目给定的数据范围肯定是会超时的，那么这时候就来想想如何优化。

在此直接得到一个数的n次方很难，那么如果先得到n/2次方再得到n次方不就简单多了吗。例如以上的示例1

要得到2的10次方就可以通过得到2的5次方，要得到2的5次方就可以先得到2的2次方，最后要得到2的2次方可以先得到2的1次方。这样就可以将要得到一大数转换为从小到大计算的过程。在此就可以发现其实我们每一步进行的过程都是一样的，那么这是就可以使用递归来解决。在此需要要得到的次方是奇数的时候再得到小的次方之后再乘一个x。

接下来就试着来将递归当中的三步分析是什么。

首先是递归当中函数头的设计，此时就要观察重复子问题当中包含哪些。通过以上的步骤图就可以看出函数需要有底数和指数。那么就可以得出函数的参数需要2个，分别是底数和指数。

接下来来分析函数体内该如何实现，也就是只需要观察一个子问题的执行流程。先得到x的n/2的结果是什么再将结果平分就得到x的n次方，当次方数为奇数的时候还要再乘一个x。

最后分析函数的出口

当n为0的时候返回1

代码实现

class Solution {
public:double myPow(double x, int n) {//判断给定的n是否小于0，是的话就需要将得到x的-n次方的结果取倒数return n<0?dfs(1.0/x,-(long long)n):dfs(x,n);}double dfs(double x,long long  n){//当n==0的时候为函数出口if(n==0)return 1;double tmp=dfs(x,n/2);return n%2==0?tmp*tmp:tmp*tmp*x;}};

注:以上dfs内函数参数x的类型设置为long long是因为题目当中n的取值范围是INT_MIN~INT_MAX，如果不使用long long在n为int最小值的时候就会出现溢出