http://noi.openjudge.cn/——2.5基本算法之搜索——1998:寻找Nemo

题目

总时间限制: 2000ms 内存限制: 65536kB
描述
Nemo 是个顽皮的小孩. 一天他一个人跑到深海里去玩. 可是他迷路了. 于是他向父亲 Marlin 发送了求救信号.通过查找地图 Marlin 发现那片海像一个有着墙和门的迷宫.所有的墙都是平行于 X 轴或 Y 轴的. 墙的厚度可以忽略不计.所有的门都开在墙上并且长度为1. Marlin 只能穿过有门的墙. 因为穿过墙是有危险的 (门旁可能会藏有巨毒的水母), Marlin 想穿过尽量少的门找到 Nemo.
图-1 显示了一个迷宫的样例及 Marlin 找到 Nemo的路线.

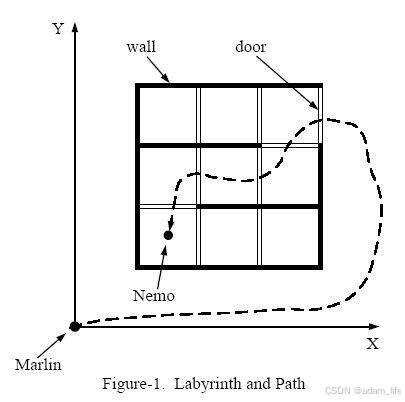
我们假设 Marlin 的初始位置在 (0, 0). 给定 Nemo 的位置和墙及门的位置情况,请你写一个程序计算 Marlin 要找到 Nemo最少要穿过多少道门.
输入
输入有多组测试数据. 每组测试数据以两个非零整数 M 和 N 开始. M 表示迷宫中墙的数目, N 表示门的数目. 接下来有 M 行, 每行包含四个整数描述一堵墙,其格式如下:
x y d t
(x, y) 表示墙的左下角, d 是墙的方向 – 0 表示它与 X-轴平行, 1 表示它与 Y-轴平行, t 表示墙的长度. 墙的两个顶点坐标在[1,199].
接下来有 N 行,用来描述门的情况:
x y d
x, y, d 与门的描述含义相同. 因为门的长度是 1, t 被省略了.
每组测试数据的最后一行包含两个正的浮点数:
f1 f2
(f1, f2) 给出了 Nemo 的位置. 它不在墙和门上.
输出
对于每组测试数据，输出一行，该行包含 Marlin 找到 Nemo需要穿过的最少的门数. 如果他不可能找到 Nemo, 输出 -1.
样例输入
8 9
1 1 1 3
2 1 1 3
3 1 1 3
4 1 1 3
1 1 0 3
1 2 0 3
1 3 0 3
1 4 0 3
2 1 1
2 2 1
2 3 1
3 1 1
3 2 1
3 3 1
1 2 0
3 3 0
4 3 1
1.5 1.5
4 0
1 1 0 1
1 1 1 1
2 1 1 1
1 2 0 1
1.5 1.7
-1 -1
样例输出
5
-1
来源
Beijing 2004 English 2049

宽搜代码

#include <bits/stdc++.h>
using namespace std;
struct room{//房间结构体 int x,y,//坐标 num;//步数少不定门少，要更新到达各房间的门数，不需要宽搜标记 bool qk[4],//左上右下右四堵墙 mk[4];//左上右下右四门 room(){//无参构造函数 memset(qk,0,sizeof(qk));memset(mk,0,sizeof(mk));//初始化，无墙无门 num=0x3f3f3f;}room(int tx,int ty):x(tx),y(ty){//两参构造函数 memset(qk,0,sizeof(qk));memset(mk,0,sizeof(mk));//初始化，无墙无门 num=0x3f3f3f;}
}p;//坐标
int m,//墙的数目n,//门的数目x,y,//墙和门的坐标（行列） d,//墙和门的方向，0水平，1垂直 t,//墙的长度 tx,ty,//nemo位置，从墙外能到达就可以。也就等于能出来就好。f[4][2]={{0,-1},{-1,0},{0,1},{1,0}},//往左上右下移动行列的变化 R,C;
float fx,fy; 
void view(room r[][200],int R,int C){cout<<"***地图\n";for(int i=0;i<=R;i++){for(int j=0;j<=C;j++){for(int x=0;x<4;x++)cout<<(r[i][j].qk[x]?(r[i][j].mk[x]?2:1):0)<<",";cout<<"\t";	}cout<<endl;}
}
int main(){//freopen("data.cpp","r",stdin);while(cin>>m>>n&&m!=-1&&n!=-1){//多组数据 R=C=0;//迷宫边界 room r[200][200];//迷宫 for(int i=0;i<200;i++)for(int j=0;j<200;j++)r[i][j]=room{i,j};//初始化迷宫各房间 for(int i=1;i<=m;i++){cin>>y>>x>>d>>t;d?(R=max(R,x+t)):(C=max(C,y+t));//修订边界 for(int j=(d?x:y);j<=(d?x:y)+t-1;j++)r[(d?j:x)][(d?y:j)].qk[d?0:1]=r[(d?j:x-1)][(d?y-1:j)].qk[d?2:3]=1;//d=0水平，那就是房间(x,j)的上墙1和(x-1,j)的下墙3//d=1垂直，那就是房间(j,y)的左墙0和(j,y-1)的右墙2}for(int i=1;i<=n;i++){cin>>y>>x>>d;r[x][y].mk[d?0:1]=r[d?x:x-1][d?y-1:y].mk[d?2:3]=1;//d=0水平，那就是房间(x,y)的上门1和(x-1,y)的下门3//d=1垂直，那就是房间(x,y)的左门0和(x,y-1)的右门2}//cout<<"边界："<<R<<"\t"<<C<<endl;//view(r,R,C);cin>>fy>>fx;//浮点数不能当整数输入，否则对后继数据的输入有影响 tx=int(fx),ty=int(fy);if(tx<1||tx>R||ty<1||ty>C){cout<<0<<endl;continue;}//需要判断是否在迷宫里，否则会访问非法空间 r[tx][ty].num=0;//刚出发，还没过门 //cout<<"总出发："<<tx<<"\t"<<ty<<endl;queue<room> q;q.push(r[tx][ty]);int ans=n+1;//从最大中找最少 while(!q.empty()){//宽搜循环 p=q.front();q.pop();//cout<<"\t出发："<<p.x<<"\t"<<p.y<<endl;if(p.x<1||p.x>R||p.y<1||p.y>C){//走到迷宫外就算成功 if(p.num<ans){ans=p.num;//cout<<"成功"<<p.x<<","<<p.y<<"\t门数"<<ans<<endl; 	}}for(int i=0;i<4;i++){//往左上右下移动 if(!r[p.x][p.y].qk[i]||r[p.x][p.y].mk[i]){//没墙或者有门就过 tx=p.x+f[i][0],ty=p.y+f[i][1];if(tx<0||tx>R||ty<0||ty>C)continue;//tx==0==R,ty==0==C是迷宫外，剪枝更外情况 if(r[tx][ty].num<=p.num+r[p.x][p.y].mk[i])continue;//剪枝门更多的情况 r[tx][ty].num=p.num+r[p.x][p.y].mk[i];//cout<<"\t\t到达："<<tx<<","<<ty<<"\t"<<r[tx][ty].num<<endl;q.push(r[tx][ty]);}}}//cout<<"结果:";if(ans==n+1)cout<<-1<<endl;else cout<<ans<<endl;}return 0;
}

优先队列

找到的第一结果就是最优解

#include <bits/stdc++.h>
using namespace std;
struct room{//房间结构体 int x,y,//坐标 num;//步数少不定门少，要更新到达各房间的门数，不需要宽搜标记 bool qk[4],//左上右下右四堵墙 mk[4];//左上右下右四门 room(){//无参构造函数 memset(qk,0,sizeof(qk));memset(mk,0,sizeof(mk));//初始化，无墙无门 num=0x3f3f3f;}room(int tx,int ty):x(tx),y(ty){//两参构造函数 memset(qk,0,sizeof(qk));memset(mk,0,sizeof(mk));//初始化，无墙无门 num=0x3f3f3f;}bool operator<(const room& r2)const{return num>r2.num;}//优先队列比较规则函数。降序返回大于情况 
}p;//坐标
int m,//墙的数目n,//门的数目x,y,//墙和门的坐标（行列） d,//墙和门的方向，0水平，1垂直 t,//墙的长度 tx,ty,//nemo位置，从墙外能到达就可以。也就等于能出来就好。f[4][2]={{0,-1},{-1,0},{0,1},{1,0}},//往左上右下移动行列的变化 R,C;
float fx,fy; 
void view(room r[][200],int R,int C){cout<<"***地图\n";for(int i=0;i<=R;i++){for(int j=0;j<=C;j++){for(int x=0;x<4;x++)cout<<(r[i][j].qk[x]?(r[i][j].mk[x]?2:1):0)<<",";cout<<"\t";	}cout<<endl;}
}
int main(){//freopen("data.cpp","r",stdin);while(cin>>m>>n&&m!=-1&&n!=-1){//多组数据 R=C=0;//迷宫边界 room r[200][200];//迷宫 for(int i=0;i<200;i++)for(int j=0;j<200;j++)r[i][j]=room{i,j};//初始化迷宫各房间 for(int i=1;i<=m;i++){cin>>y>>x>>d>>t;d?(R=max(R,x+t)):(C=max(C,y+t));//修订边界 for(int j=(d?x:y);j<=(d?x:y)+t-1;j++)r[(d?j:x)][(d?y:j)].qk[d?0:1]=r[(d?j:x-1)][(d?y-1:j)].qk[d?2:3]=1;//d=0水平，那就是房间(x,j)的上墙1和(x-1,j)的下墙3//d=1垂直，那就是房间(j,y)的左墙0和(j,y-1)的右墙2}for(int i=1;i<=n;i++){cin>>y>>x>>d;r[x][y].mk[d?0:1]=r[d?x:x-1][d?y-1:y].mk[d?2:3]=1;//d=0水平，那就是房间(x,y)的上门1和(x-1,y)的下门3//d=1垂直，那就是房间(x,y)的左门0和(x,y-1)的右门2}//cout<<"边界："<<R<<"\t"<<C<<endl;//view(r,R,C);cin>>fy>>fx;//浮点数不能当整数输入，否则对后继数据的输入有影响 tx=int(fx),ty=int(fy);if(tx<1||tx>R||ty<1||ty>C){cout<<0<<endl;continue;}//需要判断是否在迷宫里，否则会访问非法空间 r[tx][ty].num=0;//刚出发，还没过门 //cout<<"总出发："<<tx<<"\t"<<ty<<endl;priority_queue<room> q;q.push(r[tx][ty]);int ans=n+1;//从最大中找最少 while(!q.empty()){//宽搜循环 p=q.top();q.pop();//cout<<"\t出发："<<p.x<<"\t"<<p.y<<endl;if(p.x<1||p.x>R||p.y<1||p.y>C){//走到迷宫外就算成功 if(p.num<ans){//最早到达的就是最优解 ans=p.num;break;//cout<<"成功"<<p.x<<","<<p.y<<"\t门数"<<ans<<endl; 	}}for(int i=0;i<4;i++){//往左上右下移动 if(!r[p.x][p.y].qk[i]||r[p.x][p.y].mk[i]){//没墙或者有门就过 tx=p.x+f[i][0],ty=p.y+f[i][1];if(tx<0||tx>R||ty<0||ty>C)continue;//tx==0==R,ty==0==C是迷宫外，剪枝更外情况 if(r[tx][ty].num<=p.num+r[p.x][p.y].mk[i])continue;//剪枝门更多的情况 r[tx][ty].num=p.num+r[p.x][p.y].mk[i];//cout<<"\t\t到达："<<tx<<","<<ty<<"\t"<<r[tx][ty].num<<endl;q.push(r[tx][ty]);}}}//cout<<"结果:";cout<<(ans==n+1?-1:ans)<<endl;}return 0;
}

深搜代码

#include <bits/stdc++.h>
using namespace std;
struct room{//房间结构体 int x,y,//坐标 num;//步数少不定门少，要更新到达各房间的门数，不需要宽搜标记 bool qk[4],//左上右下右四堵墙 mk[4];//左上右下右四门 room(){//无参构造函数 memset(qk,0,sizeof(qk));memset(mk,0,sizeof(mk));//初始化，无墙无门 num=0x3f3f3f;}room(int tx,int ty):x(tx),y(ty){//两参构造函数 memset(qk,0,sizeof(qk));memset(mk,0,sizeof(mk));//初始化，无墙无门 num=0x3f3f3f;}bool operator<(const room& r2)const{return num>r2.num;}//优先队列比较规则函数。降序返回大于情况 
}r[200][200];//迷宫 坐标
int m,//墙的数目n,//门的数目x,y,//墙和门的坐标（行列） d,//墙和门的方向，0水平，1垂直 t,//墙的长度 tx,ty,//nemo位置，从墙外能到达就可以。也就等于能出来就好。f[4][2]={{0,-1},{-1,0},{0,1},{1,0}},//往左上右下移动行列的变化 R,C,ans;
float fx,fy; 
void view(room r[][200],int R,int C){cout<<"***地图\n";for(int i=0;i<=R;i++){for(int j=0;j<=C;j++){for(int x=0;x<4;x++)cout<<(r[i][j].qk[x]?(r[i][j].mk[x]?2:1):0)<<",";cout<<"\t";	}cout<<endl;}
}
void go(room p){if(p.x<1||p.x>R||p.y<1||p.y>C){//走到迷宫外就算成功 ans=min(ans,p.num);return;}int tx,ty;for(int i=0;i<4;i++){//往左上右下移动 if(!r[p.x][p.y].qk[i]||r[p.x][p.y].mk[i]){//没墙或者有门就过 tx=p.x+f[i][0],ty=p.y+f[i][1];if(tx<0||tx>R||ty<0||ty>C)continue;//tx==0==R,ty==0==C是迷宫外，剪枝更外情况 if(r[tx][ty].num<=p.num+p.mk[i])continue;//剪枝门更多的情况 r[tx][ty].num=p.num+p.mk[i];//cout<<"\t\t到达："<<tx<<","<<ty<<"\t"<<r[tx][ty].num<<endl;go(r[tx][ty]);}}	
}
int main(){//freopen("data.cpp","r",stdin);while(cin>>m>>n&&m!=-1&&n!=-1){//多组数据 R=C=0;//迷宫边界 for(int i=0;i<200;i++)for(int j=0;j<200;j++)r[i][j]=room{i,j};//初始化迷宫各房间 for(int i=1;i<=m;i++){cin>>y>>x>>d>>t;d?(R=max(R,x+t)):(C=max(C,y+t));//修订边界 for(int j=(d?x:y);j<=(d?x:y)+t-1;j++)r[(d?j:x)][(d?y:j)].qk[d?0:1]=r[(d?j:x-1)][(d?y-1:j)].qk[d?2:3]=1;//d=0水平，那就是房间(x,j)的上墙1和(x-1,j)的下墙3//d=1垂直，那就是房间(j,y)的左墙0和(j,y-1)的右墙2}for(int i=1;i<=n;i++){cin>>y>>x>>d;r[x][y].mk[d?0:1]=r[d?x:x-1][d?y-1:y].mk[d?2:3]=1;//d=0水平，那就是房间(x,y)的上门1和(x-1,y)的下门3//d=1垂直，那就是房间(x,y)的左门0和(x,y-1)的右门2}//cout<<"边界："<<R<<"\t"<<C<<endl;//view(r,R,C);cin>>fy>>fx;//浮点数不能当整数输入，否则对后继数据的输入有影响 tx=int(fx),ty=int(fy);if(tx<1||tx>R||ty<1||ty>C){cout<<0<<endl;continue;}//需要判断是否在迷宫里，否则会访问非法空间 r[tx][ty].num=0;//刚出发，还没过门 //cout<<"总出发："<<tx<<"\t"<<ty<<endl;ans=n+1;//从最大中找最少 go(r[tx][ty]);//cout<<"结果:";cout<<(ans==n+1?-1:ans)<<endl;}return 0;
}

小结

1.本题画地图较为麻烦，就是画墙和门。
这里要注意,输入的x、y是坐标系，就是x列y行。
静下心就可以画好
for(int j=(d?x:y);j<=(d?x:y)+t-1;j++)
r[(d?j:x)][(d?y:j)].qk[d?0:1]=r[(d?j:x-1)][(d?y-1:j)].qk[d?2:3]=1;
//d=0水平，那就是房间(x,j)的上墙1和(x-1,j)的下墙3
//d=1垂直，那就是房间(j,y)的左墙0和(j,y-1)的右墙2
2.出发的位置"f1、f2是Nemo的位置. 它不在墙和门上.",这里没说是迷宫内，所以按照位置访问数组可能会访问没申请的空间。
3.迷宫是在1到R-1,1到C-1范围内，从Nemo的位置出发，能到达0或R或C的位置就成功。而再往外可以剪枝
4.深搜和广搜是解决图论问题的基本方法，之间没有质的区别，不存在哪个方法可以解决哪个方法不能解决的问题。
相对而言
深搜：适用于需要找到一条特定路径或者所有可能路径的问题
广搜：常用于求最短路径、最少步数等问题，因为它是按照层次进行搜索的，所以第一次找到的目标节点所经过的路径一定是最短的。