代码随想录打卡|Day29 动态规划Part02（不同路径、不同路径2、整数拆分、不同的二叉树搜索）

动态规划Part02

不同路径

力扣题目链接
代码随想录链接
视频讲解链接

题目描述： 一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

思路：动态规划五步：

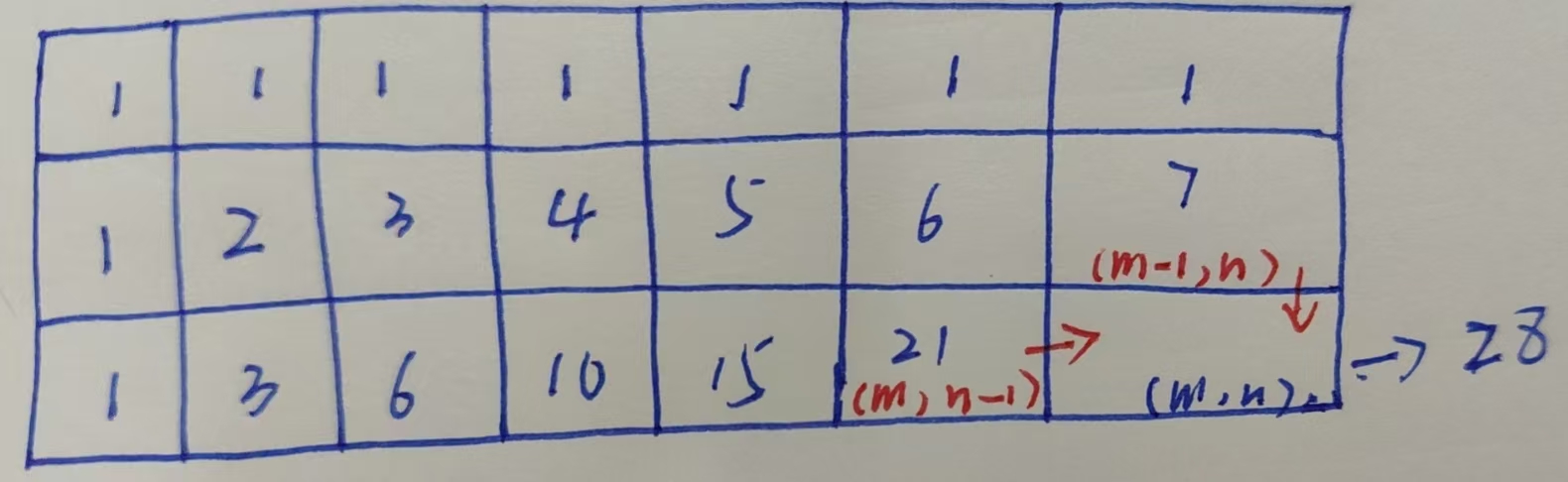
1. dp[m][n]含义：从(0,0)位置移动到(m,n)位置的所有路径
2. 递推公式：由于只能向下或者向右走，因此到达(m,n)的两个出口只可能是(m-1,n)和(m,n-1)，因此，到达(m-1,n)和(m,n-1)的路径总和就是到达(m,n)的路径总和。
3. 初始化：由于只能向右和向下走，所以当行号（i）为0的时候，无论列如何变化dp[0][j]的值始终只能为1。同理可得dp[i][0]的值也是始终只能为1.
4. 遍历顺序，行和列均从顺序2开始。
5. 打印数组。
   代码如下：

class Solution {public int uniquePaths(int m, int n) {// dp[m][n]代表从(0,0)到(m,n)一共有多少条路径int[][] dp = new int[m][n];// 初始化dp数组，由于每次只能向下或者向右走// 所以当j为0的时候，从(0,0)到(i,0)只有一种走法for(int i = 0 ; i < m ; i++) dp[i][0] = 1;// 当i为1的时候，从(0,0)到(0,j)也只有一种走法for(int j = 0 ; j < n ; j++) dp[0][j] = 1;// 对于走到(i,j)的位置，当我们有m种方法走到(i-1,j)和n种方法走到(i,j-1)的时候// 走到(i,j)位置就有m+n种方法。for(int i = 1 ; i < m ; i++){for(int j = 1 ; j < n ; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}

---

不同路径 II

力扣题目链接
代码随想录链接
视频讲解链接

题目描述： 给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。

网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。

返回机器人能够到达右下角的不同路径数量。

测试用例保证答案小于等于 2 * 109。

动态规划五步策略：

1. dp[i][j]:(0,0)到(i,j)所有的可行路径总数。
2. 递推公式：当dp[i][j]的左入口(dp[i][j-1])和上入口(dp[i-1][j])的值均不为-1的时候，dp[i][j] = dp[i-1][j] + dp[i][j-1];当左为-1，上不为-1的时候，dp[i][j] = dp[i-1][j]。当上不为-1，左为-1的时候，dp[i][j] = dp[i-1][j]，当上左均为-1的时候dp[i][j] =-1。
3. 初始化：由于只能向下或者向右走，所以当行号和列号为0的时候，我们对其赋值为1，遇到障碍物，障碍物所在格子和他的后面的格子的值均赋值为-1，代表不可通行。
4. 遍历顺序：正常行列遍历
5. 打印数组

代码如下：

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];// 初始化dp数组// 初始化列为0的时候行的值为1for(int i = 0 ; i < m ; i++){// 当行上出现障碍物之后，将该位置朝后的所有行值均赋值为-1，代表不可通行。if(obstacleGrid[i][0] == 1){dp[i][0] = -1;          if(i < m - 1)obstacleGrid[i + 1][0] = 1;}          else{dp[i][0] = 1;}}// 初始化行为0的时候列的值为1for(int j = 0 ; j < n ; j++){// 当列上出现障碍物之后，将该位置朝后的所有列值均赋值为-1，代表不可通行。if(obstacleGrid[0][j] == 1){dp[0][j] = -1;if(j < n - 1)obstacleGrid[0][j + 1] = 1;}else{dp[0][j] = 1;}}for(int i = 1 ; i < m ; i++){for(int j = 1 ; j < n ; j++){// 若不是第一行或者第一列的值为1，则将当前障碍物所在位置赋值为-1；if(obstacleGrid[i][j] == 1){dp[i][j] = -1;continue;}/**1.当dp[i - 1][j] == -1 && dp[i][j - 1] != -1，代表(i,j)位置只能从(i,j-1)处抵达。2.当dp[i - 1][j] != -1 && dp[i][j - 1] == -1，代表(i,j)位置只能从(i-1,j)处抵达。3.当dp[i - 1][j] != -1 && dp[i][j - 1] != -1，代表(i,j)位置可以从(i-1,j)和(i,j-i)抵达。4.当dp[i - 1][j] == -1 && dp[i][j - 1] == -1，代表(i,j)位置不可抵达，因此dp[i][j] = -1;*/if(dp[i - 1][j] == -1 && dp[i][j - 1] != -1){dp[i][j] = dp[i][j - 1];}else if(dp[i - 1][j] != -1 && dp[i][j - 1] == -1){dp[i][j] = dp[i - 1][j];}else if(dp[i - 1][j] != -1 && dp[i][j - 1] != -1){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}else{dp[i][j] = -1;}}}// 若dp[m - 1][n - 1] == -1，则代表(m,n)处不可抵达。所以路径数量为0；if(dp[m - 1][n - 1] == -1)return 0;return dp[m - 1][n - 1];}
}

代码随想录版本

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];//如果在起点或终点出现了障碍，直接返回0if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {return 0;}for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;}for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;}}return dp[m - 1][n - 1];}
}

优化空间版本

// 空间优化版本
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[] dp = new int[n];for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[j] = 1;}for (int i = 1; i < m; i++) {for (int j = 0; j < n; j++) {if (obstacleGrid[i][j] == 1) {dp[j] = 0;} else if (j != 0) {dp[j] += dp[j - 1];}}}return dp[n - 1];}
}

---

整数拆分（需要多理解一下）

力扣题目链接
代码随想录链接
视频讲解链接

题目描述： 给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

动态规划：

代码如下：

class Solution {public int integerBreak(int n) {//dp[i] 为正整数 i 拆分后的结果的最大乘积int[] dp = new int[n+1];dp[2] = 1;for(int i = 3; i <= n; i++) {for(int j = 1; j <= i-j; j++) {// 这里的 j 其实最大值为 i-j,再大只不过是重复而已，//并且，在本题中，我们分析 dp[0], dp[1]都是无意义的，//j 最大到 i-j,就不会用到 dp[0]与dp[1]dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));// j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘//而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。}}return dp[n];}
}

---

不同的二叉搜索树(详细讲解需要看代码随想录)

力扣题目链接
代码随想录链接
视频讲解链接

题目描述： 给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

思路：总的来说，我们需要轮流让每个节点充当root节点，每个节点当root节点的时候，其二叉搜索树额度变换形式只会由左右子树的形式所决定，即 ：左子树形式数量X右子树形式数量。最后将所有节点的形式数量和相加即可得到当前值的二叉搜索树的形式数量。

代码如下：

class Solution {public int numTrees(int n) {int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for(int i = 2 ; i <= n ; i++){for(int j = 1 ; j <= i ; j++){dp[i] += dp[j - 1] * dp[i-j];}}return dp[n];}
}

---